Question
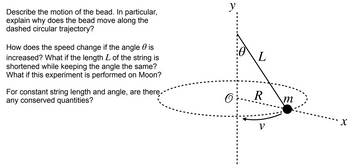
Transcribed Image Text:Describe the motion of the bead. In particular,
explain why does the bead move along the
dashed circular trajectory?
How does the speed change if the angle is
increased? What if the length L of the string is
shortened while keeping the angle the same?
What if this experiment is performed on Moon?
For constant string length and angle, are there
any conserved quantities?
y
O
L
R
V
m
X
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Similar questions
- A bob of mass m is suspended from a fixed point with a massless string of length L (i.e., it is a pendulum). You are to investigate the motion in which the string moves in a cone with half-angle θ. a. What tangential speed, v, must the bob have so that it moves in a horizontal circle with the string always making an angle θ from the vertical? b. How long does it take the bob to make one full revolution (one complete trip around the circle)? Express your answer in terms of some or all of the variables m, L, and θ, as well as the free-fall acceleration g.arrow_forwardLearning Goal: To find some of the parameters characterizing an object moving in a circular orbit. The motivation for Isaac Newton to discover his laws of motion was to explain the properties of planetary orbits that were observed by Tycho Brahe and analyzed by Johannes Kepler. A good starting point for understanding this (as well as the speed of the space shuttle and the height of geostationary satellites) is the simplest orbit: a circular one. This problem concerns the properties of circular orbits for a satellite orbiting a planet of mass M. For all parts of this problem, where appropriate, use G for the universal gravitational constant. Part A Find the orbital speed v of a satellite in a circular orbit of radius R around a planet of mass M. Express the orbital speed in terms of G, M, and R. ► View Available Hint(s) V = Submit Part B K = Find the kinetic energy K of a satellite with mass m in a circular orbit of radius R around a planet of mass M. Express your answer in terms of m,…arrow_forwardHow do you get part Carrow_forward
- 1. Consider the arbitrarily shaped object shown in the figure to the right undergoing a uniform circular motion in the xy plane about a fixed axis that is perpendicular to the xy plane. Point O is located in the xy plane along the axis of rotation and P is a fixed point on the object located at a distance r from the point O. If the magnitude of velocity vector of point P is v= 1.3 m/s, and the radius of its circular path is r = 0.65 m, determine: (a) The angular velocity w of point P (b) The magnitude of acceleration vector a of point P 20 P narrow_forwardNumber 8 to 9 are togetherarrow_forwardThanks!!arrow_forward
- A 20.0 kg child is on a swing that hangs from 3.00-m-long chains, as shown in (Figure 1). Figure 3.0 m 45° 1 of 1arrow_forwardYou have put a sonar device at the top of a frictionless inclined plane, as shown in the diagram below. That device allows you to measure the distance an object is from the device, as well as the speed and the acceleration of that object. If we decide that the origin (h = 0) is at the sonar device, we want to know what the height change is as we slide down the incline. 0 For an angle below the horizontal of 6.46, we see that our object has slid a distance 1.13 m, as measured along the incline itself. Calculate the height change in meters - and report your answer as a negative number. (This value would be useful for calculating the change in gravitational potential energy, as we will do in the lab.) h=o 10% O i 26 QUATU 99+ hp X 55 83°F 3:11 PM 10/16/2022 Ctrl 0arrow_forwardA student is swinging a ball of mass 0.323 kg in a vertical circle at constant speed, as shown in the figure below. (g indicates the direction of the acceleration due to gravity: directly downward.) The length of the string is 0.76 m. She measures the tension and finds that it is 5.601 times larger at the bottom of the circle than at the top. What is the speed of the swinging mass?arrow_forward
- Assuming negligible atmospheric friction, a launched projectile has a parabolic path, as shown above. Point Q is the path peak and Points P and R are at the same altitude. Identify the correct relationship of the projectile speeds at the three points. O A. vp = VR < VQ O B. VO < VR < vP OC.Vo< vp = VR O D. VR < VQ < vP O E. Vp < VQ < VRarrow_forwardLearning Goal: To find some of the parameters characterizing an object moving in a circular orbit. The motivation for Isaac Newton to discover his laws of motion was to explain the properties of planetary orbits that were observed by Tycho Brahe and analyzed by Johannes Kepler. A good starting point for understanding this (as well as the speed of the space shuttle and the height of geostationary satellites) is the simplest orbit: a circular one. This problem concerns the properties of circular orbits for a satellite orbiting a planet of mass M. For all parts of this problem, where appropriate, use G for the universal gravitational constant. The potential energy U of an object of mass m that is separated by a distance R from an object of mass M is given by U=-G Mm R What is the kinetic energy K of the satellite? Express your answer in terms of the potential energy U. K = Submit Part D T = Find the satellite's orbital period T. Express your answer in terms of G, M, R, and T. ► View…arrow_forwardHello, Can someone please show how to solve this problem? Thanksarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios