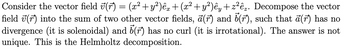
Consider the vector field ʊ(r) = (x² + y²)êx + (x² + y²)êy + z²êz. Decompose the vector field (r) into the sum of two other vector fields, a (r) and 5(r), such that a(r) has no divergence (it is solenoidal) and 5 (r) has no curl (it is irrotational). The answer is not unique. This is the Helmholtz decomposition.

Consider the special shape pictured in the diagram below. It is a cylinder, centered on the origin with its axis oriented along z, and it has been partially hollowed to leave two cone-shaped cavities at the top and bottom of the cylinder. The radius of the object is a, its height is 2a, and the solid part of the object (the shaded region that is visible in the rightmost panel of the illustration above, which shows a drawing of the cross-section of the object) has a uniform volume charge density of po. Assume that the object is spinning counter clockwise about its cylinder axis at an angular frequency of w. Which of the following operations is part of the calculation of the magnitude of the current density that is associated with the motion of the rotating object as a function of r (select all that apply)?

Find the electric flux crossing the wire frame ABCD of length , width b and whose center is at a distance OP = d from an infinite line of charge with linear charge density λ. Consider that the plane of frame is perpendicular to the line OP (Fig. ). A d Fig. A D b P 8 C

The electric field in a region of space near the origin is given by E(z, y, :) – E, (*) yî+ xî a (a) Evaluate the curl Vx E(x, y, z) (b) Setting V(0, 0, 0) = 0, select a path from (0,0, 0) to (x, y, 0) and compute V (r, y,0). (c) Sketch the four distinct equipotential lines that pass through the four points (a, a), (-a, a), (-a, -a), and (a, -a). Label each line by the value of V.