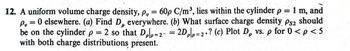
12. A uniform volume charge density, p, = 60p C/m³, lies within the cylinder p = 1 m, and P, = 0 elsewhere. (a) Find D, everywhere. (b) What surface charge density Ps2 should be on the cylinder p = 2 so that Dolp=2- = 2Dplp=2+? (c) Plot D, vs. p for 0 < p < 5 with both charge distributions present.

pls answer number 1 and pls show a clear solution ty.

(a) A solid sphere, made of an insulating material, has a volume charge density of p where r is the radius from the center of the sphere, a is constant, and a > 0. What is the electric field within the sphere as a function of the radius r? Note: The volume element dv for a spherical shell of radius r and thickness dr is equal to 4xr2dr. (Use the following as necessary: a, r, and g.) magnitude direction E = direction a %0 magnitude E = a Use a gaussian surface concentric with the sphere. How much charge is enclosed by the surface? Can you integrate over the spherical volume, using the given distribution and volume element, to find the charge? How does Gauss's law relate this charge to the flux? Using spherical symmetry, how can you relate the flux to the electric field and the area of the sphere? radially outward (b) What If? What if the charge density as a function of r within the charged solid sphere is given by p electric field within the sphere at radius r. (Use the following as…

An infinite cylinder of radius R has a charge density given by p(r) = ar", where r is the perpendicular distance from the axis of the cylinder, and a is a constant. Show that the electric field for r > R given by aR E(r) 7€or satisfies V ·Ē = 0 for r > R. Explain briefly why this condition must be obeyed.

A 2D annulus (thick ring) has an inner radius Ri and outer radius Ro, and charge Q non-uniformlydistributed over its surface. The 2D charge density varies with radius r by η(r)=Cr 4 for Ri ≤ r ≤ Roand η=0 for all other r. C is a constant. Answer the following in terms of the variables given above. Note: Gauss' Law will not be useful here.a) Find an expression for C such that the total charge of the annulus is Q. Include the SI units for C next to your answer.Do the units make sense?b) Draw a clear picture and use it to set up the integral to calculate the E-field at a point on the axis of the annulus (this axis is perpendicular to the plane of the annulus) a distance z from the center of the annulus. *** You must complete all the steps short of computing the integral (i.e. your eventual answer must be an integral with only ONE variable of integration and all other variables constant.) Show that your answer has the correct SI units for the electric field.

An infinitely long insulating cylinder of radius R has a volume charge density that varies with the radius as given by the following expression where pa, and are positive consta axis of the cylinder p-p(0-1) Use Gauss's law to determine the magnitude of the electric field at the following radial distances. (Use the following as necessary: Po, b, c, and R.) (a) R EM Po x 2R (-36) 200 x

A disk with radius R has uniform surface charge density σ.

A disk of radius R and mass M has a nonuniform surface charge density sigma = Cr, where C is a constant and r is measured from the center of the disk. find the constant c in terms of the mass M and R?

A charge of 7.60 pC is spread uniformly throughout the volume of a sphere of radiusr= 4.15 cm. What is the magnitude of the %3D electric field at a radial distance of (a)6.29 cm and (b)3.23 cm?

Find the total charge contained in a cylindrical volume defined by ρ ≤ 2 m and 0 ≤ z ≤ 3 m if ρv = 20 ρz (mC/m3)