Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN: 9780133923605
Author: Robert L. Boylestad
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Related questions
Question
thumb_up100%
can you explain to me why the convolution of these two sinc fucntions which are rect functions equal a rect function? I thought when you convolute a rectangle and a rectangle with two different lengths, it makes a trapezoid shape. The answer says it is rectangle funtion so my code is corrcect but i dont understand why this is true. I need a step by step solution and explanation.
here is the problem: Consider the signal x(t) = 2 sinc(6t + 3).
the output y (t) = (x *h )(t) when x(t) is
passed through a filter with impulse response h (t) = 4sinc(2t -1). the matlab code was just to help me visuallize
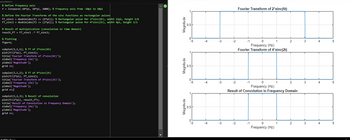
Transcribed Image Text:we/untitled.m
% Define frequency axis
f = linspace(-10*pi, 10*pi, 1000); % Frequency axis from -10pi to 10pi
% Define the Fourier Transforms of the sinc functions as rectangular pulses
FT_sinc1 = double(abs(f) <= (6*pi)); % Rectangular pulse for 2*sinc(6t), width 12pi, height 1/6
FT_sinc2 = double(abs(f) <= (2*pi)); % Rectangular pulse for 4*sinc(2t), width 4pi, height 1/2
% Result of multiplication (convolution in time domain)
result_FT = FT_sinc1 .* FT_sinc2;
% Plotting
figure;
subplot(3,1,1); % FT of 2*sinc(6t)
plot(f/(2*pi), FT_sinc1);
title('Fourier Transform of 2*sinc(6t)');
xlabel('Frequency (Hz)');
ylabel('Magnitude');
grid on;
subplot(3,1,2); % FT of 4*sinc(2t)
plot(f/(2*pi), FT_sinc2);
title('Fourier Transform of 4*sinc(2t)');
xlabel('Frequency (Hz)');
ylabel('Magnitude');
grid on;
subplot(3,1,3); % Result of convolution
plot(f/(2*pi), result_FT);
title('Result of Convolution in Frequency Domain');
xlabel('Frequency (Hz)');
ylabel('Magnitude');
grid on;
d Window.
Magnitude
Magnitude
0.5
Magnitude
0.5
Fourier Transform of 2*sinc(6t)
0
-3
-2
-1
-4
-3
-2
0
Frequency (Hz)
Fourier Transform of 4*sinc(2t)
0
Frequency (Hz)
Result of Convolution in Frequency Domain
2
3
5
2
3
4
5
-5
-3
-2
-1
0
2
3
4
5
Frequency (Hz)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 5 steps with 3 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, electrical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Typing solution please I will like it please ASAP Pleasearrow_forwardSS 6-43 For the circuit in Figure P6-43, find an equivalent circuit consisting of one inductor and one capacitor. Select a value of an inductor and a capacitor from among the standard values in Appendix G to realize your result and connect them appropriately. 0.005 µF 0.005 µF LEQ, CEQ 25 μΗ 33 ΜΗ 15 pH FIGURE P6-43 5000 pFarrow_forwardFor the R-C circuit in Figure, composed of standard values: I would like to check my answer Determine the time constant of the circuit when the switch is throwninto position 1. I got 0.2s Find the mathematical expression for the voltage across the capacitorand the current after the switch is thrown into position 1. I got Vc = 8V(1-e-t/0.2s) ic = 4e-t/0.2smA And for the Determine the magnitude of the voltage vC and the current iC the instantthe switch is thrown into position 2 at t = 1 s. I got Vc = 7.95V and Ic = 0.02695mA Can you check if its correctarrow_forward
- 18 E = 35V R1 R1 = R2 = 50 %3D %3D R4 R3 = 150 35 V R3 R4 = R5 = R6 = 100 Determine la I que pasa por la batería. R5 R6 R2arrow_forwardWhat are phasors and what is this equation?arrow_forward6-38 The switch in the circuit of Figure P6-38 is closed at t = 0, and the circuit is ini- tially relaxed. Determine the current i(t). FIGURE P6-38 100 cos 5000f 0.2 H 1.2 k ww 190² 0.2 μFarrow_forward
- could you help me with these questions thank youarrow_forwardRequired information NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Consider a 3 mH inductor. Determine the voltage developed across the 3 mH inductor if the current is 15 e-nA. (You must provide an answer before moving on to the next part.) The voltage developed across 3 mH inductor is x10-12 e-tv. Adaptive SYNC D B F wwwwwwwwwww H T Q Search ren IA CD O 11:40 PM 0 4/19/2023 /// 2 0 a 9 W 4 1212arrow_forwardFind Req . Using wye-delta Transformation . The answer is .( Req= 28.5 ) I know the answer but please make the steps clear and the diagrams clear . Thank u Please answer in typing format please ASAP forarrow_forward
- Hello. I keep getting weird answers and I don't think I am going about this correctly. Could you help me out with this problem? Thank you for your timarrow_forwardNeeded to be solved this question correctly in 10 minutes and get the thumbs up please solve correctly in the order to get positive feedback I need accuracy any how pleasearrow_forwardb) Derive a block diagram model for the RLC series circuit shown in Figure Q1, relating input voltage Vin to output voltage Vout derived across the inductor. Your answer should identify the state variables, list the governing equations, and clearly show the direction of flow of signals in the block diagram. R + Vin(~ C Figure Q1 0.000 Voutarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education 
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:PEARSON
Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:9781337900348
Author:Stephen L. Herman
Publisher:Cengage Learning
Programmable Logic Controllers
Electrical Engineering
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education
Fundamentals of Electric Circuits
Electrical Engineering
ISBN:9780078028229
Author:Charles K Alexander, Matthew Sadiku
Publisher:McGraw-Hill Education
Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:9780134746968
Author:James W. Nilsson, Susan Riedel
Publisher:PEARSON
Engineering Electromagnetics
Electrical Engineering
ISBN:9780078028151
Author:Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:Mcgraw-hill Education,