Consider a cylindrical distribution of charge whose base coincides with the plane z = 0 and axis on the z-axis. The cylindrical surface has a length L with radius rho and has a uniform charge distribution rho s C/m^2 on its surface. The aim is to determine the electric field intensity at a distance P(0, 0, h). Please draw the figure describing the problem.
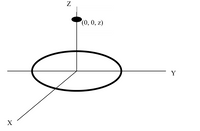
A. Related to the problem, the electric field intensity of the z-axis of a ring of charge shown in pic 2 is in pic 1. How can we prove such equation?
B. Now, if you take a strip on the cylindrical surface in a form of a ring, a distance z from the origin with a differential height of dz, what is then the differential expression of electric field intensity ( dE ) at point P? Show the diagram for the extracted differential strip.
C. With the same problem, what is the expression of d rhoL?
D. With the same problem also, to find E vector at point P, we intergrate dE vector at (B) from z = 0 to z = L. What then is E vector?
E. Lastly for the same problem, what is E at h= 0, at h = L/2 and at h= L.
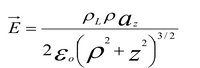
Step by stepSolved in 4 steps with 4 images

Please finish D and E.
Please finish D and E.
- show detailsarrow_forwardConducting Sphere 6 v.A If a total charge of +9.6 C accumulates on the inner surface of the hollow sphere (i.e. the cavity wall), what must be the charge Q of the enclosed point charge? Enter the numerical value in SI units. Type your answer... 7 metal What is the direction of the electric field at point P? A point charge Q is located in an enclosed cavity within a hollow conducting metal sphere. The region in the cavity between the point charge and the sphere is empty space. Point P is completely within the metal. O The electric field at point P is zero. O The direction depends on the value of the charge on the outer surface of the sphere.arrow_forwardy The figure above shows a contour consisting of two semicircular parts, of radii a and b respectively (b> a), that are connected by two short straight-line segments. This contour has a uniform charge distribution p₁ on it. Determine the electric field created by this charge distribution at the origin of the coordinate system in terms of a, b, and P₁-arrow_forward
- An infinitely long rod lies along the x-axis and carries a uniform linear charge density λ = 5 μC/m. A hollow cone segment of height H = 27 cm lies concentric with the x-axis. The end around the origin has a radius R1 = 8 cm and the far end has a radius R2 = 16 cm. Refer to the figure. a. Consider the conic surface to be sliced vertically into an infinite number of rings, each of radius r and infinitesimal thickness dx. Enter an expression for the electric flux differential through one of these infinitesimal rings in terms of λ, x, and the Coulomb constant k. b. Integrate the electric flux over the length of the cone to find an expression for the total flux through the curved part of the cone (not including the top and bottom) in terms of λ, H, and the Coulomb constant k. Enter the expression you find. c. Calculate the electric flux, in N•m2/C, through the circular end of the cone at x = 0. d. Calculate the electric flux, in N•m2/C, through the circular end of the cone at x = H. e.…arrow_forwardA long coaxial cable carries a volume charge density described by p = ks4 (where k is a constant) on the inner insulating cylinder (radius a), and a uniform surface charge density ? (sigma) on the outer conducting cylindrical shell (radius b). Assume that the coaxial cable is electrically neutral (i.e. Qtotal = 0) and you may ignore the edge effects of the cylindrical shells.a. Determine the electric field everywhere in terms of the total charge per unit length of the inner cylinder ?inner (lambdainner).arrow_forwardThe electric flux through a spherical Gaussian surface of radius r=20.0cm, with a uniformly charged, spherical conducting shell at its center, is ΦE =−2.30 × 104 N·m2/C. T c. How many excess electrons or protons does this sphere contain? d. f the conductor has a radius of R = 10.0 cm, what is its surface charge density? e. What is the electric field strength at the surface of the conductor?arrow_forward
- A nonconducting, thin plane sheet of charge carries a uniform charge per unit area of 5.20 µC/m2 as in the figure below.(a) Find the electric field at a distance of 8.70 cm from the plate.(b) Explain whether your result changes as the distance from the sheet is varied. Earrow_forwardI Review A positive point charge q sits at the center of a hollow spherical shell. The shell, with radius R and negligible thickness, has net charge -2q. Part A Find an expression for the electric field strength inside the sphere, r R. Give your answer as a multiple of q/e0. ? Submit Request Answer 圓arrow_forward