
Engineering Fundamentals: An Introduction to Engineering (MindTap Course List)
5th Edition
ISBN: 9781305084766
Author: Saeed Moaveni
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Please show all steps
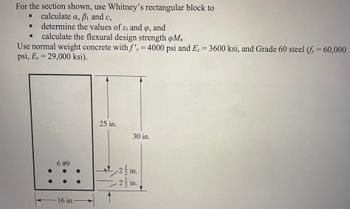
Transcribed Image Text:### Structural Engineering Problem: Calculating Flexural Design Strength
#### Objective:
For the section shown, use Whitney’s rectangular block to:
- Calculate \( a \), \( \beta_1 \), and \( c \),
- Determine the values of \( \epsilon_t \) and \( \phi \),
- Calculate the flexural design strength \( \phi M_n \).
#### Given Parameters:
- Use normal weight concrete with \( f'_c = 4000 \text{ psi} \) and \( E_c = 3600 \text{ ksi} \),
- Grade 60 steel (\( f_y = 60,000 \text{ psi} \), \( E_s = 29,000 \text{ ksi} \)).
#### Diagram Description:
A rectangular cross-section is illustrated as follows:
- The width of the section is 16 inches.
- The overall height of the section is 30 inches.
- There are 6 reinforcement bars depicted as circles, each labeled as #9.
- The depth of concrete cover from the top and the bottom of the section to the reinforcement is \( 2 \frac{1}{2} \) inches.
- The depth to the centroid of the reinforcement steel bars is specified as 25 inches from the top.
#### Detailed Steps for Calculation:
1. **Determine the depth parameters \( a \), \( \beta_1 \), and \( c \):
- Use the given concrete and steel properties and refer to the respective codes or standards to determine these values.
2. **Calculate \( \epsilon_t \) and \( \phi \):
- Utilize strain compatibility and force equilibrium methods to determine the tensile strain \( \epsilon_t \).
- Use appropriate design codes to find the strength reduction factor \( \phi \).
3. **Compute the flexural design strength \( \phi M_n \):
- Apply the calculated values into the design equations to find the nominal moment capacity and multiply by \( \phi \) to obtain the flexural design strength.
#### References:
- Structural engineering design codes (e.g., ACI 318).
This problem helps in understanding how to apply fundamental principles of reinforced concrete design, particularly in calculating the flexural strength of a concrete section with reinforcement. The figures provided alongside the mathematical approach help visualize and solve the problem effectively.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
can you explain why in solving for d the 2.5in was divided by 2
Solution
by Bartleby Expert
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
can you explain why in solving for d the 2.5in was divided by 2
Solution
by Bartleby Expert
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.Similar questions
Recommended textbooks for you
 Engineering Fundamentals: An Introduction to Engi...Civil EngineeringISBN:9781305084766Author:Saeed MoaveniPublisher:Cengage Learning
Engineering Fundamentals: An Introduction to Engi...Civil EngineeringISBN:9781305084766Author:Saeed MoaveniPublisher:Cengage Learning Architectural Drafting and Design (MindTap Course...Civil EngineeringISBN:9781285165738Author:Alan Jefferis, David A. Madsen, David P. MadsenPublisher:Cengage Learning
Architectural Drafting and Design (MindTap Course...Civil EngineeringISBN:9781285165738Author:Alan Jefferis, David A. Madsen, David P. MadsenPublisher:Cengage Learning Fundamentals Of Construction EstimatingCivil EngineeringISBN:9781337399395Author:Pratt, David J.Publisher:Cengage,
Fundamentals Of Construction EstimatingCivil EngineeringISBN:9781337399395Author:Pratt, David J.Publisher:Cengage, Solid Waste EngineeringCivil EngineeringISBN:9781305635203Author:Worrell, William A.Publisher:Cengage Learning,
Solid Waste EngineeringCivil EngineeringISBN:9781305635203Author:Worrell, William A.Publisher:Cengage Learning, Construction Materials, Methods and Techniques (M...Civil EngineeringISBN:9781305086272Author:William P. Spence, Eva KultermannPublisher:Cengage Learning
Construction Materials, Methods and Techniques (M...Civil EngineeringISBN:9781305086272Author:William P. Spence, Eva KultermannPublisher:Cengage Learning Residential Construction Academy: House Wiring (M...Civil EngineeringISBN:9781285852225Author:Gregory W FletcherPublisher:Cengage Learning
Residential Construction Academy: House Wiring (M...Civil EngineeringISBN:9781285852225Author:Gregory W FletcherPublisher:Cengage Learning

Engineering Fundamentals: An Introduction to Engi...
Civil Engineering
ISBN:9781305084766
Author:Saeed Moaveni
Publisher:Cengage Learning

Architectural Drafting and Design (MindTap Course...
Civil Engineering
ISBN:9781285165738
Author:Alan Jefferis, David A. Madsen, David P. Madsen
Publisher:Cengage Learning

Fundamentals Of Construction Estimating
Civil Engineering
ISBN:9781337399395
Author:Pratt, David J.
Publisher:Cengage,

Solid Waste Engineering
Civil Engineering
ISBN:9781305635203
Author:Worrell, William A.
Publisher:Cengage Learning,

Construction Materials, Methods and Techniques (M...
Civil Engineering
ISBN:9781305086272
Author:William P. Spence, Eva Kultermann
Publisher:Cengage Learning

Residential Construction Academy: House Wiring (M...
Civil Engineering
ISBN:9781285852225
Author:Gregory W Fletcher
Publisher:Cengage Learning