Problem 1RQ: Define and explain the differences between the following terms. a. law and theory b. theory and... Problem 2RQ: Is the scientific method suitable for solving problems only in the sciences? Explain. Problem 3RQ: Which of the following statements could be tested by quantitative measurement? a. Ty Cobb was a... Problem 4RQ: For each of the following pieces of glassware, provide sample measurement and discuss the number of... Problem 5RQ: A student performed an analysis of a sample for its calcium content and got the following results:... Problem 6RQ: Compare and contrast the multiplication/division significant figure rule to the significant figure... Problem 7RQ: Explain how density can be used as a conversion factor to convert the volume of an object to the... Problem 8RQ: On which temperature scale (F, C. or K) docs 1 degree represent the smallest change in temperature? Problem 9RQ: Distinguish between physical changes and chemical changes. Problem 10RQ: Why is the separation of mixtures into pure or relatively pure substances so important when... Problem 1ALQ: a. There are 365 days per year, 24 hours per day, 12 months per year, and 60 minutes per hour. Use... Problem 2ALQ Problem 3ALQ: When a marble is dropped into a beaker of water, it sinks to the bottom. Which of the following is... Problem 4ALQ Problem 5ALQ: You may have noticed that when water boils, you can see bubbles that rise to the surface of the... Problem 6ALQ: If you place a glass rod over a burning candle, the glass appears to turn black. What is happening... Problem 7ALQ: Which characteristics of a solid, a liquid, and a gas are exhibited by each of the following... Problem 8ALQ: Sketch a magnified view (showing atoms/molecules) of each of the following and explain: a. a... Problem 9ALQ: Paracelsus, a sixteenth-century alchemist and healer, adopted as his slogan: "The patients are your... Problem 10ALQ: What is wrong with the following statement? "The results of the experiment do not agree with the... Problem 11ALQ: Why is it incorrect to say that the results of a measurement were accurate but not precise? Problem 14ALQ: You have a 1.0-cm3 sample of lead and a 1.0-cm3 sample of glass. You drop each in separate beakers... Problem 15ALQ: Consider the addition of 15.4 to 28. What would a mathematician say the answer is? What would a... Problem 16ALQ: Consider multiplying 26.2 by 16.43. What would a mathematician say the answer is? What would a... Problem 17ALQ: True or false? For mathematical operation performed on two measurements, the number of significant... Problem 18ALQ: Is there a difference between a homogeneous mixture of hydrogen and oxygen in a 2:1 ratio and a... Problem 19Q: The difference between a law and a theory is the difference between what and why. Explain. Problem 20Q: The scientific method is a dynamic process. What does this mean? Problem 21Q: Explain the fundamental steps of the scientific method. Problem 22Q Problem 23Q: A measurement is a quantitative observation involving both a number and a unit. What is a... Problem 24Q: To determine the volume of a cube, a student measured one of the dimensions of the cube several... Problem 25Q: What are significant figures? Show how to indicate the number one thousand to 1 significant figure,... Problem 26Q: A cold front moves through and the temperature drops by 20 degrees. In which temperature scale would... Problem 28Q: In a multiple-step calculation, is it better to round off the numbers to the correct number of... Problem 29Q: Is the density of a gaseous substance larger or smaller than the density of a liquid or a solid at... Problem 30Q: Give four examples illustrating each of the following terms. a. homogeneous mixture b. heterogeneous... Problem 31E: Which of the following are exact numbers? a. There are 100 cm in 1 m. b. One meter equals 1.094... Problem 32E: Indicate the number of significant figures in each of the following: a. This book contains more than... Problem 33E: How many significant figures are there in each of die following values? a. 6.07 1015 b. 0.003840 c.... Problem 34E: How many significant figures are in each of the following? a. 100 b. 102 c. 103 d. 100. e. 0.0048... Problem 35E: Round off each of the following numbers to the indicated number of significant digits, and write the... Problem 36E: Use exponential notation to express the number 385,500 to a. one significant figure. b. two... Problem 37E: You have liquid in each graduated cylinder shown: You then add both samples to a beaker. How would... Problem 38E: The beakers shown below have different precisions. a. Label the amount of water in each of the three... Problem 39E: Evaluate each of the following, and write the answer to the appropriate number of significant... Problem 40E: Perform the following mathematical operations, and express each result to the correct number of... Problem 41E: Perform the following mathematical operations, and express the result to the correct number of... Problem 42E: Perform the following mathematical operations, and express the result to the correct number of... Problem 43E: Perform each of the following conversions. a. 8.43 cm to millimeters b. 2.41 102 cm to meters c.... Problem 44E: a. How many kilograms are in 1 teragram? b. How many nanometers are in 6.50 x 102 terameters? c. How... Problem 45E: Perform the following unit conversions. a. Congratulations! You and your spouse are the proud... Problem 46E: Perform the following unit conversions. a. 908 oz to kilograms b. 12.8 L to gallons c. 125 mL to... Problem 47E: Use the following exact conversion factors to perform the stated calculations: 512 yd -= 1 rod 40... Problem 48E: Although the preferred SI unit of area is the square meter, land is often measured in the metric... Problem 49E: Precious metals and gems are measured in troy weights in the English system: 24 grains 1 pennyweight... Problem 50E: Apothecaries (druggists) use the following set of measures in the English system: 20 grains ap = 1... Problem 51E: For a pharmacist dispensing pills or capsules, it is often easier to weigh the medication to be... Problem 52E: A children's pain relief elixir contains 80. mg acetaminophen per 0.50 teaspoon. The dosage... Problem 53E: Science fiction often uses nautical analogies to describe space travel. If the starship U.S.S.... Problem 54E: The world record for the hundred meter dash is 9.58 s. What is the corresponding average speed in... Problem 55E: You are driving 65 mi/h and take your eyes off the road for just a second. What distance (in feet)... Problem 56E: You pass a road sign saying New York 112 km. If you drive at a constant speed of 65 mi/h, how long... Problem 57E: The dosage for an antibiotic is prescribed at 8.0 mg per kilo-gram of body weight, taken twice daily... Problem 58E: In recent years, there has been a large push for an increase in the use of renewable resources to... Problem 59E Problem 60E: Carbon monoxide (CO) detectors sound an alarm when peak levels of carbon monoxide reach 100 parts... Problem 61E: Convert the following Fahrenheit temperatures to the Celsius and Kelvin scales. a. 459F, an... Problem 62E: A thermometer gives a reading of 96.1F 0.2F. What is the temperature in C? What is the uncertainty? Problem 63E: Convert the following Celsius temperatures to Kelvin and to Fahrenheit degrees. a. the temperature... Problem 64E: Convert the following Kelvin temperatures to Celsius and Fahrenheit degrees. a. the temperature that... Problem 65E: At what temperature is the temperature in degrees Fahrenheit equal to twice the temperature in... Problem 66E: The average daytime temperatures on the earth and Jupiter are 72F and 313 K, respectively. Calculate... Problem 67E: Use the figure below to answer the following questions. a. Derive the relationship between C and X.... Problem 68E: Ethylene glycol is the main component in automobile anti-freeze. To monitor the temperature of an... Problem 69E: A material will float on the surface of a liquid if the material has a density less than that of the... Problem 70E: One metal object is a cube with edges of 3.00 cm and a mass of 140.4 g. A second metal object is a... Problem 71E: A star is estimated to have a mass of 2 1036 kg. Assuming it to be a sphere of average radius 7.0 ... Problem 72E: A rectangular block has dimensions 2.9 cm 3.5 cm 10.0 cm. The mass of the block is 615.0 g. What... Problem 73E: Diamonds are measured in carats, and 1 carat = 0.200 g. The density of diamond is 3.51 g/cm3. a.... Problem 74E: At room temperature the element bromine, Br2, is a liquid with a density of 3.12 g/cm3. Calculate... Problem 75E: A sample containing 33.42 g of metal pellets is poured into a graduated cylinder initially... Problem 76E: The density of pure silver is 10.5 g/cm3 at 20C. If 5.25 g of pure silver pellets is added to a... Problem 77E: In e-ach of the following pairs, which has the greater mass? (See Table 1.5.) a. 1.0 kg of feathers... Problem 78E: a. Calculate the mass of ethanol in 1.50 qt of ethanol. (See Table 1.5.) b. Calculate the mass of... Problem 79E: In each of the following pairs, which has the greater volume? a. 1.0 kg of feathers or 1.0 kg of... Problem 80E: Using Table 1.5, calculate the volume of 25.0 g of each of the following substances at 1 atm. a.... Problem 81E: The density of osmium (the densest metal) is 22.57 g/cm3. If a 1.00-kg rectangular block of osmium... Problem 82E: A copper wire (density = 8.96 g/cm3) has a diameter of 0.25 mm. If a sample of this copper wire has... Problem 83E: Match each description below with the following microscopic pictures. More than one picture may fit... Problem 84E: Define the following terms: solid, liquid, gas, pure substance, element, compound, homogeneous... Problem 85E: What is the difference between homogeneous and heterogeneous matter? Classify each of the following... Problem 86E: Classify the following mixtures as homogeneous or heterogeneous. a. potting soil b. white wine c.... Problem 87E: Classify each of the following as a mixture or a pure substance. a. water b. blood c. the oceans d.... Problem 88E: Suppose a teaspoon of magnesium filings and a teaspoon of powdered sulfur are placed together in a... Problem 89E: If a piece of hard, white blackboard chalk is heated strongly in a flame, the mass of the piece of... Problem 90E: During a very cold winter, the temperature may remain below freezing for extended periods. However,... Problem 91E: Classify the following as physical or chemical changes. a. Moth balls gradually vaporize in a... Problem 92E: The properties of a mixture are typically averages of the properties of its components. The... Problem 93AE: Two spherical objects have the same mass. One floats on water; the other sinks. Which object has the... Problem 94AE: A 194-g sample of caffeine (C8H10N4O2) contains 6.02 1023 molecules of caffeine. If a typical... Problem 95AE: Lipitor, a pharmaceutical drug that has been shown to lower bad cholesterol levels while raising... Problem 96AE: In Shakespeares Richard III, the First Murderer says: Take that, and that! [Stabs Clarence] If that... Problem 97AE Problem 98AE: In the opening scenes of the movie Raiders of the Lost Ark, Indiana Jones tries to remove a gold... Problem 99AE Problem 100AE: The active ingredient of aspirin tablets is acetylsalicylic acid, which, has a density of 1.4 g/cm3.... Problem 101AE: This year, like many past years, you begin to feel very sleepy alter eating a large helping of... Problem 102AE: Which of the following are chemical changes? Which are physical changes? a. the cutting of food b.... Problem 103AE: A person with high cholesterol has 250 mg of cholesterol per 100.0 mL of blood. If the total blood... Problem 104AE Problem 105AE: A column of liquid is found to expand linearly on heating. Assume the column rises 5.25 cm for a... Problem 106AE: A 25.00-g sample of a solid is placed in a graduated cylinder, and then the cylinder is filled to... Problem 107AE: For each of the following, decide which block is more dense; the orange block, the blue block, or it... Problem 108AE: According to the Official Rules of Baseball, a baseball must have a circumference not more than 9.25... Problem 109AE: The density of an irregularly shaped object was determined as follows. The mass of the object was... Problem 110AE: The chemist in Example 1.14 did some further experiments. She found that the pipet used to measure... Problem 111CWP: The longest river in the world is the Nile River with a length of 4145 mi. How long is the Nile in... Problem 112CWP: Secretariat is known as the horse with the fastest run in the Kentucky Derby. If Secretariats record... Problem 113CWP: The hottest temperature recorded in the United States is 134F in Greenland Ranch, CA. The melting... Problem 114CWP Problem 115CWP: Which of the following statements is(are) true? a. A spoonful of sugar is a mixture. b. Only... Problem 116CWP: Which of the following describes a chemical property? a. The density of iron is 7.87 g/cm3. b. A... Problem 117CP: A rule of thumb in designing experiments is to avoid using a result that is the small difference... Problem 118CP: Draw a picture showing the markings (graduations) on glassware that would allow you to make each of... Problem 119CP: Many times errors are expressed in terms of percentage. The percent error is die absolute value of... Problem 120CP: A person weighed 15 pennies on a balance and recorded the following masses: 3.112 g 3.109 g 3.059 g... Problem 121CP: On October 21, 1982, the Bureau of the Mint changed the composition of pennies (see Exercise 120).... Problem 122CP: As part of a science project, you study traffic patterns in your city at an intersection in the... Problem 123CP: Sterling silver is a solid solution of silver and copper. If a piece of a sterling silver necklace... Problem 124CP: Make molecular-level (microscopic) drawings for each of the following. a. Show the differences... Problem 125CP: Confronted with the box shown in the diagram, you wish to discover something about its internal... format_list_bulleted

![The image contains the mathematical expression for the hydrogen 1s wavefunction. It is represented as follows:
\[ \psi_{1s} = \frac{1}{\sqrt{\pi}} \left( \frac{1}{a_0} \right)^{3/2} e^{-r/a_0} \]
**Explanation:**
- **ψ_{1s}**: This represents the wavefunction for the 1s orbital of a hydrogen atom.
- **π**: Represents the mathematical constant pi, approximately equal to 3.14159.
- **a_0**: Known as the Bohr radius, it is a physical constant approximately equal to 0.529 Ångströms.
- **r**: The radial distance from the nucleus.
- **e^{-r/a_0}**: An exponential decay factor that describes how the wavefunction decreases with increasing distance from the nucleus.
This formula is fundamental in quantum mechanics for understanding electron distribution in a hydrogen atom.](https://content.bartleby.com/qna-images/question/c297b31e-0a8f-4ccd-8e08-7779ed8f9d82/cbb91650-b087-4cc0-8a23-521f59175d81/eav3htg_thumbnail.jpeg)

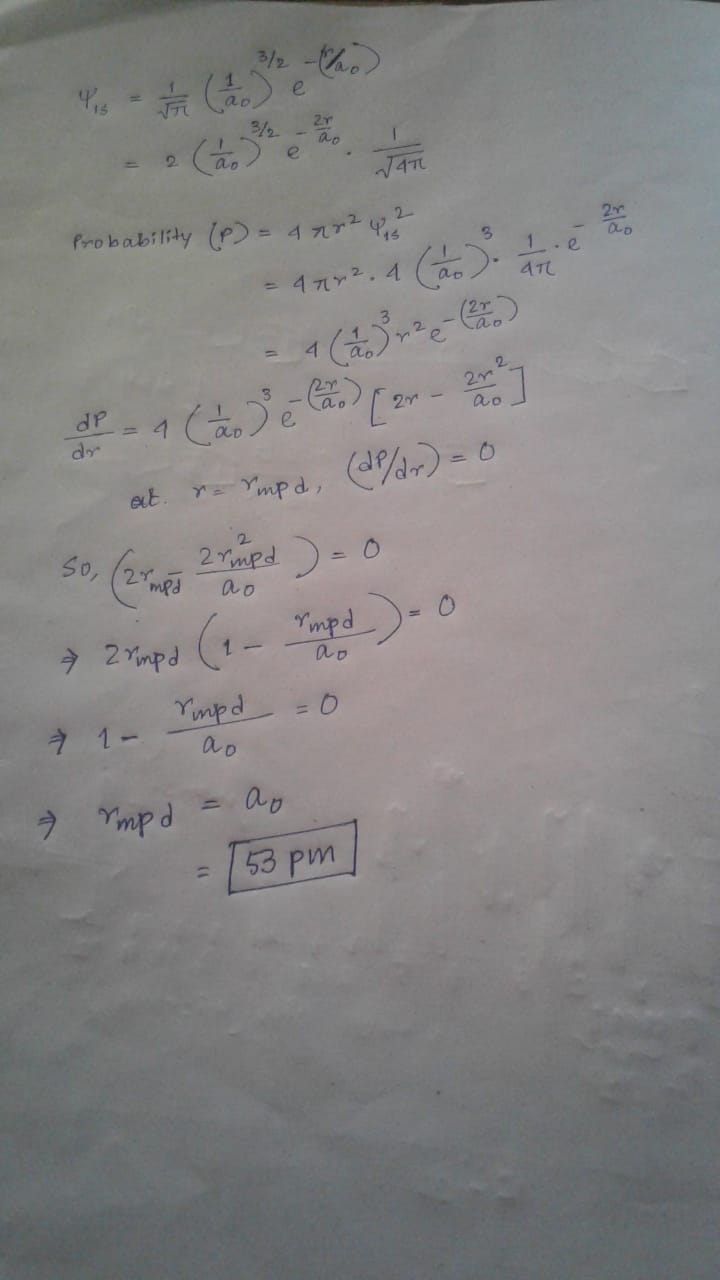

 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education
ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning
Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education
Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY




