BO -[0] C Let A = where B and C are square. Show that A is invertible if and only if bath B and C are invertible. DE [] FG Carry out the multiplication on the left and right side. First, suppose that A is invertible and let A¹ AA ВО DE 0 C FG BD BE CF CG CO It has been stated that A Then AA ВО D O C F G Since B is square, according to the Invertible Matrix Theorem the equation BD-I implies that B is invertible. Since C is square, according to the Invertible Matrix Theorem the equation CG I implies that C is invertible. Left-multiply both sides of the equation BE-0 by B¹ to get E=B¹0=0. -1 Left-multiply both sides of the equation CF=0 by C to get F-C¹0=0. (9 Therefore, it can be stated that A -х X+
BO -[0] C Let A = where B and C are square. Show that A is invertible if and only if bath B and C are invertible. DE [] FG Carry out the multiplication on the left and right side. First, suppose that A is invertible and let A¹ AA ВО DE 0 C FG BD BE CF CG CO It has been stated that A Then AA ВО D O C F G Since B is square, according to the Invertible Matrix Theorem the equation BD-I implies that B is invertible. Since C is square, according to the Invertible Matrix Theorem the equation CG I implies that C is invertible. Left-multiply both sides of the equation BE-0 by B¹ to get E=B¹0=0. -1 Left-multiply both sides of the equation CF=0 by C to get F-C¹0=0. (9 Therefore, it can be stated that A -х X+
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![BO
-[0]
C
Let A =
where B and C are square. Show that A is invertible if and only if bath B and C are invertible.
First, suppose that A is invertible and let A¹
AA
Carry out the multiplication on the left and right side.
DE
ВО
0 C FG
BD BE
CF CG
CO
DE
ВО
D
[]~-~~~~ [[|]
Then AA
FG
C
F G
It has been stated that A
Since B is square, according to the Invertible Matrix Theorem the equation BD-I implies that B is invertible.
Since C is square, according to the Invertible Matrix Theorem the equation CG I implies that C is invertible.
Left-multiply both sides of the equation BE-0 by B¹ to get E=B¹0=0.
-1
Left-multiply both sides of the equation CF=0 by C to get F-C¹0=0.
[],
Therefore, it can be stated that A
(2²4) + X](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F101db870-ee2e-4aa4-9595-a6c70c5a50a9%2F990373b1-d132-4a71-ad64-c6907515b082%2Fm2nl4cf_processed.png&w=3840&q=75)
Transcribed Image Text:BO
-[0]
C
Let A =
where B and C are square. Show that A is invertible if and only if bath B and C are invertible.
First, suppose that A is invertible and let A¹
AA
Carry out the multiplication on the left and right side.
DE
ВО
0 C FG
BD BE
CF CG
CO
DE
ВО
D
[]~-~~~~ [[|]
Then AA
FG
C
F G
It has been stated that A
Since B is square, according to the Invertible Matrix Theorem the equation BD-I implies that B is invertible.
Since C is square, according to the Invertible Matrix Theorem the equation CG I implies that C is invertible.
Left-multiply both sides of the equation BE-0 by B¹ to get E=B¹0=0.
-1
Left-multiply both sides of the equation CF=0 by C to get F-C¹0=0.
[],
Therefore, it can be stated that A
(2²4) + X
Expert Solution
Step 1
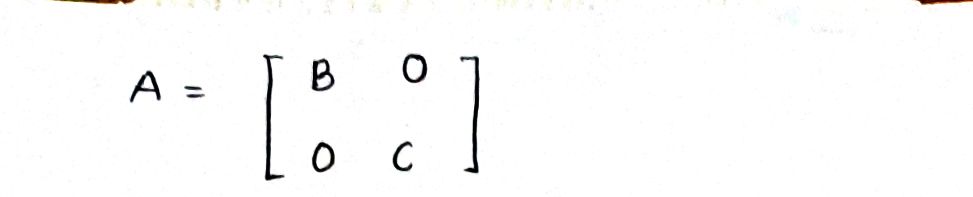
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

