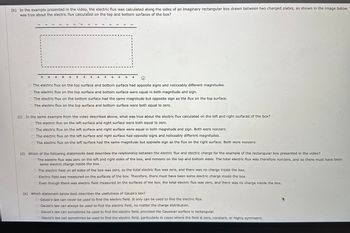
(b) In the example presented in the video, the electric flux was calculated along the sides of an imaginary rectangular box drawn between two charged plates, as shown in the image bele was true about the electric flux calculated on the top and bottom surfaces of the box? + + + + + + + + + + + + The electric flux on the top surface and bottom surface had opposite signs and noticeably different magnitudes. The electric flux on the top surface and bottom surface were equal in both magnitude and sign. The electric flux on the bottom surface had the same magnitude but opposite sign as the flux on the top surface. O The electric flux on the top surface and bottom surface were both equal to zero. (c) In the same example from the video described above, what was true about the electric flux calculated on the left and right surfaces of the box? The electric flux on the left surface and right surface were both equal to zero. The electric flux on the left surface and right surface were equal in both magnitude and sign. Both were nonzero. The electric flux on the left surface and right surface had opposite signs and noticeably different magnitudes. The electric flux on the left surface had the same magnitude but opposite sign as the flux on the right surface. Both were nonzero. (d) Which of the following statements best describes the relationship between the electric flux and electric charge for the example of the rectangular box presented in the video? The electric flux was zero on the left and right sides of the box, and nonzero on the top and bottom sides. The total electric flux was therefore nonzero, and so there must have been some electric charge inside the box. The electric field on all sides of the box was zero, so the total electric flux was zero, and there was no charge inside the box. Electric field was measured on the surfaces of the box. Therefore, there must have been some electric charge inside the box. Even though there was electric field measured on the surfaces of the box, the total electric flux was zero, and there was no charge inside the box. (e) Which statement below best describes the usefulness of Gauss's law? OGauss's law can never be used to find the electric field. It only can be used to find the electric flux. Gauss's law can always be used to find the electric field, no matter the charge distribution. Gauss's law can sometimes be used to find the electric field, provided the Gaussian surface is rectangular. Gauss's law can sometimes be used to find the electric field, particularly in cases where the field is zero, constant, or highly symmetric.

Gisha has been given a vector function which describes an electric field. Aid gisha in determining the electric flux trougheach of the three surfaces sections depicted below. E = 21+x²ĵ a x a N a a a y

Consider a closed triangular box resting within a horizontal electric field of magnitude E = 7.14 x 104 N/C as shown in the figure below. 30.0 cm 60.0° 10.0 cm (a) Calculate the electric flux through the vertical rectangular surface of the box. | kN - m²/c (b) Calculate the electric flux through the slanted surface of the box. kN - m2/c (c) Calculate the electric flux through the entire surface of the box. | kN - m²/c

Find the electric field at location P in the image:

At what angle do electric lines of force enter and leave a charged surface for maximum electric flux?     Select one: a.  60°  b.  0° c. 90° d. 30°

The electric field E, at one face of a parallelopiped is uni- form over the entire face and is directed out of the face. At the opposite face, the electric field E2 is also uniform over the entire face and is directed into that face (as shown in Fig. ). The two faces in question are inclined at 30° from the horizontal, while E, and E₂ (both horizon- tal) have magnitudes of 2.50 x 104 N/C and 7.00 × 104 N/C. Assuming that no other electric field lines cross the surfaces of the parallelopiped, determine the net charge contained within. a. -67.5 80 C c. 105 o C : 005 E₁ *74 کار کیا Fig. 6.00 cm LL b. 37.5 80 C d. - 105 & C E₂ 30°