College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Related questions
Concept explainers
Question
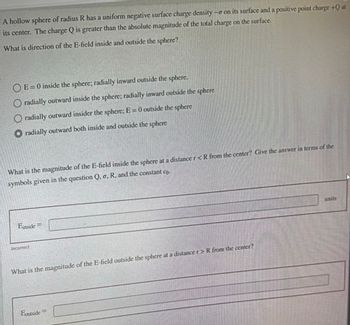
A hollow sphere of radui R has a uniform nagative surface charge density -\sigma on its surface and a positive point charge +Q at its center. The charge Q is greater than the absolute magnitude of the total charge on the surface. The direction of the E-field is radially outward both inside and outside the sphere.
What is the magnitude of the E-field inside the sphere at a distance r<R from the center?
What is the magnitude of the E-field outside the sphere at a distance r<R from the center?
Transcribed Image Text:A hollow sphere of radius R has a uniform negative surface charge density -o on its surface and a positive point charge +Q at
its center. The charge Q is greater than the absolute magnitude of the total charge on the surface.
What is direction of the E-field inside and outside the sphere?
E=0 inside the sphere; radially inward outside the sphere.
Oradially outward inside the sphere; radially inward outside the sphere
radially outward insider the sphere; E = 0 outside the sphere
radially outward both inside and outside the sphere
What is the magnitude of the E-field inside the sphere at a distance r < R from the center? Give the answer in terms of the
symbols given in the question Q, o, R, and the constant co-
Einside =
Incorrect
What is the magnitude of the E-field outside the sphere at a distance r > R from the center?
Eoutside =
units
D
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps with 3 images
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r> R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4πRªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 TR²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4Rªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 TR²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4πRªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 TR²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4Rªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 TR²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4Rªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 1¬R²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4Rªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 1¬R²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4πRªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 1¬R²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4πRªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 TR²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4Rªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 TR²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r> R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4Rªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 1¬R²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r> R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4πRªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 TR²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4Rªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 TR²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4πRªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 TR²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4Rªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 TR²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4Rªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 1¬R²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4Rªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 1¬R²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4πRªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 1¬R²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4πRªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 TR²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r > R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4Rªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 TR²G
4760
R²o
Solution
by Bartleby Expert
Follow-up Question
Step 3: Electric Field Outside the Sphere answer is incorrect. Can we try again?
Transcribed Image Text:O
Step 3: Electric Field Outside the Sphere
Electric Field Outside the Sphere (r> R)
Outside the sphere, the negative surface charge - on the sphere contributes
to the electric field.
Using Gauss's Law and a Gaussian surface in the shape of a sphere with
radius r (r > R) centered at the center of the sphere, we can find the electric
field due to the negative surface charge.
The charge enclosed within this Gaussian surface is the total charge on the
surface, which is −4Rªo.
Therefore, by Gauss's Law, the magnitude of the electric field outside the
sphere at a distance r > R from the center is:
Eoutside
1 1¬R²G
4760
R²o
Solution
by Bartleby Expert
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Please please type the answer instead of writing, thanksarrow_forwardAn infinite sheet charge of has a charge density of +25.9 pC/m-and covers the entire x-y plane. A second infinite sheet of charge ha a charge density of -58.6 pC/m2 covers the entire y-z plane. What is the magnitude of the electric field at any point not on either surface?arrow_forwardA hollow conducting sphere has an inside radius of r1 = 0.17 m and an exterior radius of r2 = 0.27 m. The sphere has a net charge of Q = 5.4E-06 C. What is the field E1 in N/C 1 m from the sphere's exterior surface? What is the magnitude of the field at a distance of 0.05 m from the center of the sphere?arrow_forward
- The entire y axis is covered with a uniform linear charge density 2.2 nC/m. Determine the magnitude of the electric field on the x axis at x= 5.5 m.arrow_forwardThe figure shows a solid non-conducting sphere of radius a = 4.4 cm. It is surrounded by a charged conducting spherical shell of inner radius b = 15.3 cm and outer radius c = 24.8 cm. The inner sphere has a net charge of q1 = 9 nC and the conducting spherical shell has a net charge of q2 = -7 nC. a. What is the surface charge density on the inside surface of the spherical shell? b. What is the surface charge density on the outside surface of the spherical shell? c. What is the value of the electric field at a distance r = 58 cm from the centre of the spheres? Please use a negative value to indicate the electric field points toward the centre of the spheres and a positive value to indicate away from the centre of the spheres.arrow_forwardA charge of uniform linear density 2.00 nC/m is distributed along a long, thin, nonconducting rod. The rod is coaxial with a long conducting cylindrical shell (inner radius = 4.20 cm, outer radius = 9.80 cm). The net charge on the shell is zero. (a) What is the magnitude of the electric field at distance r = 14.0 cm from the axis of the shell? What is the surface charge density on the (b) inner and (c) outer surface of the shell?arrow_forward
- A total amount of positive charge Q is spread onto a thin non-conducting circular annulus of inner radius a and outer radius b. The charge is distributed in a way so that the charge density per unit area is given by ? =??3, where r is the distance from the center of the annulus to any point on it and k is a constant.(a) Find an expression for the total charge Q on the annulus. (b) Find an expression for the potential V at the center of the annulus in term of Q, a and barrow_forwardA thin, copper washer of inner radius R = 54.0 mm and width d = 27.0 mm carries a unformly distributed total charge Q-9.00 nC. Determine the z-component of the electric field, Ez, due to the washer at a distance z = 12.0 cm along the washer's symmetry axis. Ez = -7.99 ×104 Incorrect N/C y Zarrow_forwardA cube has positive charge +Q in all corners except for one, which has a negative point charge - Q. Let the distance from any corner to the center of the cube be r. What is the magnitude and direction of the of electric field at the center of the cube (point P)?arrow_forward
- There are two uncharged concentric conducting spherical shells and a separate point charge. The smaller shell has an inner radius of 0.100m and an outer radius of 0.200m. The larger shell has an inner radius of 0.300m and and outer radius of 0.400m. A point charge of +10.0μC is placed between the two shells at a radius of 0.250m from the origin. Determine the net charge on each of the four surfaces (r = 0.1,0.2, 0.3, 0.4) and make a sketch that indicates BOTH the electric field lines and the surface charge densities. (this sketch does not have to be exactly mathematically correct, but use intuition)arrow_forwardThe figure shows a hollow metal sphere with inner radius 6.70 cm and outer radius 13.5 cm and a point charge at the center. The inner surface of the hollow sphere has a total charge of 3.70 nC and the outer surface has a total charge of -15.5 nC. Calculate the magnitude electric field a distance 18.0 cm from the center of the sphere.arrow_forwardThe question is in the picture.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press 
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON
Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON