
Introduction to Chemical Engineering Thermodynamics
8th Edition
ISBN: 9781259696527
Author: J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark Swihart
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Question
Attaching question and figure, please solve a,b,c and then i will post it once again for the remaining parts.

Transcribed Image Text:As shown in Figure A, two immiscible, incompressible liquids are flowing
in the x-direction (streamwise direction) in a horizontal thin slit of length L
and width W under the influence of a horizontal pressure gradient (
Po – P1/L). The fluid flow rates are adjusted, so that the slit is half filled with
liquid I (the less dense phase) and half filled with liquid II (the more dense
phase). The liquids are flowing sufficiently slowly that no instabilities occur -
that is, the interface remains exactly planar. This is a steady state flow of two
Newtonian liquids with constant viscosities and densities, which is studied in
Cartesian coordinates. Gravitational effects are not important.
(a) Identify the streamwise, transverse and spanwise direction of the flow
(b) Identify which velocity component is non zero for this flow problem
(c) Formulate the continuity equation for both phases and check what
information you obtain
(d) Formulate the momentum conservation eq. in the spanwise direction and
check what information you obtain (for both phases)
(e) Formulate the momentum conservation equation in the transverse
direction and check what information you obtain (for both phases)
(f) Formulate the momentum conservation equation in the streamwise
direction and determine the velocity profiles as well as the shear stress (for
both phases)
(g) Draw a figure with the resulting velocity profiles and the shear stress. How
is the position of zero shear stress associated with the profile of the
velocities?
А.
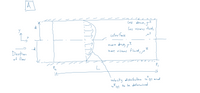
Transcribed Image Text:A
Less dense, s
Less viscous fluid,
cuter face
more deuse, p
more vis cous fluid,
Diredian
of flow
velocity distribution un aud
to be defermiued
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 4 images

Knowledge Booster
Similar questions
- this isnt what was asked. also copied and pasted from other question could someone show clearer working for 1 and 2 please i am not sure where the (4v+1) comes fromarrow_forwardWhy is a linear calibration curve important? Couldn't interpolation be used to predict values within the calibration range?arrow_forwardStuck need help! Problem is attached. please view attachment before answering. Really struggling with this concept. Please show all work so I can better understand ! Thank you so much.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education
Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
 Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning
Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The
Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The

Introduction to Chemical Engineering Thermodynami...
Chemical Engineering
ISBN:9781259696527
Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark Swihart
Publisher:McGraw-Hill Education

Elementary Principles of Chemical Processes, Bind...
Chemical Engineering
ISBN:9781118431221
Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. Bullard
Publisher:WILEY

Elements of Chemical Reaction Engineering (5th Ed...
Chemical Engineering
ISBN:9780133887518
Author:H. Scott Fogler
Publisher:Prentice Hall


Industrial Plastics: Theory and Applications
Chemical Engineering
ISBN:9781285061238
Author:Lokensgard, Erik
Publisher:Delmar Cengage Learning

Unit Operations of Chemical Engineering
Chemical Engineering
ISBN:9780072848236
Author:Warren McCabe, Julian C. Smith, Peter Harriott
Publisher:McGraw-Hill Companies, The