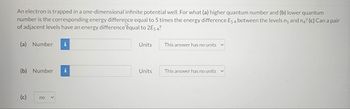
An electron is trapped in a one-dimensional infinite potential well. For what (a) higher quantum number and (b) lower quantum number is the corresponding energy difference equal to 5 times the energy difference E54 between the levels ng and n4? (c) Can a pair of adjacent levels have an energy difference equal to 2E5 4? (a) Number i (b) Number Units Units This answer has no units This answer has no units

3. Particle in a 2D Box. A quantum mechanical particle is confined in side a square 2D box, with side length L. Inside the box V=0 and outside the box V=infinity. Let the wave function to be (x,y). (a) write down the Schrodinger equation of (x,y). (b) Use the separation of variable method solve (x,y) (let the quantum numbers to be nx and ny.) (c) What is the energy for the state (nx, ny)? (d) What is the probability density p(x,y) for the state nx=3 and ny=3? Sketch this p(x,y) in a square.

3) A Particle Trapped in a Shallow Defect This is a simple model for a shallow trap or defect in a semiconductor, for example, or a more realistic model for a quantum dot. We are interested in the trap states, i.e., states where the particle is localized in the trap. Hence this requires E 0 dij(x) dx √x = - 1²/2 2 din(x) dx = For the odd solution, use the following solution with A' = - C': 4₁(x) = A' exx (x) = {₁(x) = B′ sin kx B' m(x)=C'e-xx III = din(x) dx You should also apply in each case the continuity conditions: 4₁ (x = -²2 ) = ₁ (x = -1) Pu (x=+) = m(x=+) dpm(x) dx |x=+12/2 VI 8 -- / x VI 212 x≤ - 1²/12 ≤x≤ 11/27 ≤ x |x=+23/23 Use these conditions in the solution to find a set of two homogeneous equations of two unknowns. Solve these equations to find a relation between k and K and plot the solutions on a graph.

7. One electron is trapped in a one-dimensional square well potential with infinitely high sides. a. If you have a probe that has a width for electron detection Ax = 0.00350L in the x direction, for the first excited state ( n =2), what is the probability that the electron is found in the probe when it is centered at x = L/4, (hint: you can use an approximation for this - you do not need to do an integral)? b. What is the average number of electrons that you would detect using the probe described in part "b." centered at x = L/4, ifthe electron is in the first excited state (n = 2) for each experiment and you repeat the experiment N, =100,000 times?