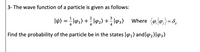
3- The wave function of a particle is given as follows: I) = lø1) +l92) + l93) Where (ol0,)=ô, Find the probability of the particle be in the states |91) and|92)l93)

3.)  A classical ball bounces back and forth between two rigid walls with no loss of speed. After a long time has passed, the ball's position is measured at a random time. a. Is the probability Prob(inA)that the ball is found in sectionAlarger than, smaller than, or the same as the probability Prob(in B) of being found in section B?

3) A Particle Trapped in a Shallow Defect This is a simple model for a shallow trap or defect in a semiconductor, for example, or a more realistic model for a quantum dot. We are interested in the trap states, i.e., states where the particle is localized in the trap. Hence this requires E 0 dij(x) dx √x = - 1²/2 2 din(x) dx = For the odd solution, use the following solution with A' = - C': 4₁(x) = A' exx (x) = {₁(x) = B′ sin kx B' m(x)=C'e-xx III = din(x) dx You should also apply in each case the continuity conditions: 4₁ (x = -²2 ) = ₁ (x = -1) Pu (x=+) = m(x=+) dpm(x) dx |x=+12/2 VI 8 -- / x VI 212 x≤ - 1²/12 ≤x≤ 11/27 ≤ x |x=+23/23 Use these conditions in the solution to find a set of two homogeneous equations of two unknowns. Solve these equations to find a relation between k and K and plot the solutions on a graph.

16. Consider the wave function Mx) = (alT)" exp(-ax12) Calculate (x) for n = 1, 2. Can you quickly write down the result for (")?