Question
An 87 kg
person stands on a uniform ladder 4.0 m
long, that weighs 90 N
, as shown in the figure(Figure 1). The floor is rough; hence, it exerts both a normal force, f1
, and a frictional force, f2
, on the ladder. The wall, on the other hand, is frictionless; it exerts only a normal force, f3
.
A) Find the forces exerted on the ladder when the person is three-fourths of the way up the ladder.
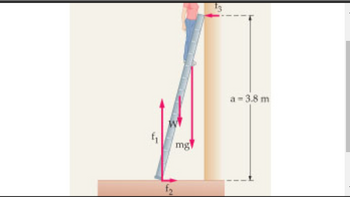
Transcribed Image Text:f₁
2
mg
a-3.8 m
Expert Solution
arrow_forward
Step 1
Given,
mass of a person m = 87 kg
length of uniform ladder L = 4.0 m
weight of ladder W2 = 90 N
man is at a distance of three-fourths of a way up the ladder.
weight of the ladder acts in the middle of the ladder.
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- An object of mass m has these three forces acting on it (there is no normal torce, "no surface"). F₁, F2, and F3 as shown in the figure on the right. When answering the questions below, assume the x-direction is to the right, and the y-direction is straight upwards. F=F₂i-r1-F₁j ✔Correct! ||F| = F← ➤F₂ Write a symbolic expression for the net force in component form. Give your answer in terms of F₁, F2, F3, and the unit vectors i and j. Let F₁ =3 N, F₂ = 10 N, and F3 = 1 N. Calculate is the magnitude of the net force, in newtons. sin() cos() tan() 7 8 9 HOME T() EMA cotan() asin() 5 6 atan() * acotan() 1 2 cosh() tanh() 0 END CLEAR Ⓒ Degrees VO BACKSPACE DEL Submit Hint Feedback I give up! What is the angle 8, in degrees, of the net force, measured from the +x-axis? Enter an angle between -180° and 180°. What is the magnitude, al of the acceleration, in meters per square second, if the block has a mass of 7.6 kg? acos sinh() cotanh() Radians +4 1 wa 3 ISarrow_forwardA certain orthodontist uses a wire brace to align a patient's crooked tooth as in the figure below. The tension in the wire is adjusted to have a magnitude of 12.5 N. Find the magnitude of the net force exerted by the wire on the crooked tooth.arrow_forwardOne straightforward way to measure the coefficients of friction between a box and a wooden surface is illustrated in (Figure 1). The sheet of wood can be raised by pivoting it about one edge. It is first raised to an angle θ1 (which is measured) for which the box just begins to slide downward. The sheet is then immediately lowered to an angle θ2 (which is also measured) for which the box slides with constant speed down the sheet. Part A) Apply Newton’s second law to the box to find the coefficient of static friction between it and the wooden sheet. Express your answer in terms of some or all of the variables θ1 and θ2. Part B) Apply Newton’s second law to the box to find the coefficient of kinetic friction between it and the wooden sheet. Express your answer in terms of some or all of the variables θ1 and θ2.arrow_forward
- Two weights are hanging from the ceiling of an elevator as shown in (Figure 1). Find the tension in cable A when the elevator is not moving. Express your answer in newtons. Find the tension in cable B when the elevator is not moving. Express your answer in newtons. Find the tension in cable B when the elevator is accelerating downward at 1.4 m/s2. Express your answer in newtons. Find the tension in cable A when the elevator is accelerating downward at 1.4 m/s2. Express your answer in newtons.arrow_forwardBe sure all quantities are expressed in standard units before calculating anything. Thank you :)arrow_forwardI Review Part A Find the tension in the string connecting mj and m2. Assume the table is frictionless and the masses move freely. (Figure 1) Express your answer using two significant figures. Υ ΑΣΦ T = Submit Request Answer Figure 1 of 1 Part B m, = 1.0 kg m2 = 2.0 kg Find the tension in the string connecting m2 and m3. Express your answer using two significant figures. m, = 3.0 kg 0 ΑΣφ T2 = Pearsonarrow_forward
- The pulley system shown in the figure (Figure 1) is used to lift a 52-kg crate. Note that one chain connects the upper pulley to the ceiling and a second chain connects the lower pulley to the crate. The crate is rising with an acceleration of 2.6 m/s2. a) Assuming the masses of the chains, pulleys, and ropes are negligible, determine the magnitude of the force F→. b) Determine the tension in the upper chain. c) Determine the tension in the lower chain.arrow_forwardBoxes A and B are connected to each end of a light vertical rope, as shown in the following figure. A constant upward force 80.0 N is applied to box A. Starting from rest, box B descends 11.5 m in 4.50 s. The tension in the rope connecting the two boxes is 32.0 N (Figure 1). Figure F A B 1 of 1 Part A What is the mass of box B? Express your answer with the appropriate units. MB = Submit Part B mA = Submit μA Provide Feedback Value Request Answer What is the mass of box A? Express your answer with the appropriate units. μA Value → Request Answer Units Units ? ?arrow_forwardhe FBD of the block should have looked like this. 1. A contestant in a winter sporting event pushes a block of ice of mass m across a frozen lake as shown in the figure. The coefficient of static friction between the block and ice is μs, and the coefficient of kinetic friction is μk. θ is the angle the force makes with the x-axis. In this part, we are going to set-up Newton's second Law equations for the cases(1) when the ice block just starts moving, and(2) when it is accelerating to the right with an acceleration a. All answers are symbolic. ALL ANSWERS ARE CASE-SENSITIVE. Subpart 1: Newton's Second Law along the y-axis (i) Write Newton's Second Law along the y-axis by adding all forces in the y-direction taking into account their signs (forces pointing upwards are positive and downward are negative) in terms of the normal force N, weight mg, F and θ. In both scenarios, there is no acceleration along the y-direction, therefore, ay=0.…arrow_forward
- Please look at the picture to be able to answer the following questions. Question 1: If FT is the force of tension in one side of the line, which of the following represents the total force of the line on the woman in the y direction? a. FT sin θ b. 2 FT cos θ c. FT cos θ d. 2 FT sin θ Question 2: Which of the following is the most useful formulation of Newton's 2nd Law in the y direction? a. mg + 2 FT cos θ = 0 b. mg - 2 FT sin θ = ma y c. mg + 2 FT sin θ = 0 d. mg - 2 FT sin θ = 0 Question 3: What is the magnitude of the tension force in one side of the line? Assume g = 9.8 m/s^2 and answer in N. Please answer all three questions....arrow_forwardTwo identical 20.0-kg balls, each 25.3 cm in diameter, are suspended by two 35.0-cm wires as shown in the figure (Figure 1). The entire apparatus is supported by a single 18.0-cm wire, and the surfaces of the balls are perfectly smooth. Find the tension in the top wire. Find the tension in each of two bottom wires.arrow_forwardM Support Cable 37° M As shown in the diagram above, a rigid rod of mass M is hinged at its left end against a wall. A block of mass M hangs on the right edge of the rod. A support cable attached to the right end of the rod forms an angle of 37 degrees with horizontal. The tension in the string is 1,057 N. Calculate the mass M of the rod and the block. Express your answer in kilograms and round to the nearest tenth (1 decimal).arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios