Computer Networking: A Top-Down Approach (7th Edition)
7th Edition
ISBN: 9780133594140
Author: James Kurose, Keith Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Related questions
Question
Given the Nondeterministic Finite Automaton (NFA). Need help proving, by induction on n, that for all positive integers n, the string (aba)n is accepted by this NFA. (This string is obtained by n repetitions of aba.) Thank you :)
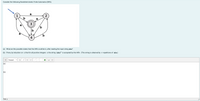
Transcribed Image Text:Consider the following Nondeterministic Finite Automaton (NFA).
a
1
a
a
4
(a) What are the possible states that this NFA could be in, after reading the input string aba?
(b) Prove, by induction on n, that for all positive integers n, the string (aba)" is accepted by this NFA. (This string is obtained by n repetitions of aba.)
Paragraph
B
(a)
|(b)
Path: p
3.
Expert Solution
arrow_forward
Step 1
(a) There are two possible states after string (aba)^n, that is
1. 1 -> a -> 2 -> b -> 4 -> a -> 1, which is non final state
2. Final state, 1 -> a -> 4 -> b -> 2 -> a -> 3
Step by stepSolved in 2 steps
Knowledge Booster
Similar questions
- Design a deterministic finite automaton for the given regular expression R. R = (0 + 1 (1 + 01) *00) *arrow_forwardWe want to prove that f(n) = 1/n² +8√n + 1 is O(n²) using the formal definition introduced in class (i.e f(n) is O(g(n)) if there are two constant c and no such that f(n) ≤ c · g(n) for all n ≥ no). Which of the following pair(s) of constants c and no satisfy the definition? C = and no = C = 21 2 C = 19 and no 2 R 1/2 and no c = 10 and no = 1000 P = A. TA B 0 Consider the string s="BARBAPAPA". Which of the following trees is/are representing the optimal prefix codes obtained by the Huffman Algorithm? (Reminder: an edge to the left child encodes a 0, while an edge to the right child encodes a 1). 1 = = 4 A A 101010110110 10101001010110110 01100001100110011 R B 100001100011001100 B. TB P A) (R B P C. Tc A Using the codes from above, which of the following bit strings are valid encoding of s using Huffman Encoding? B R P D. Tparrow_forwardWhat is the time complexity of a program with functions and procedure calls? Given two distinct functions f(n) and g(n) prove that f(n) = O(g(n)). Can Ω be used instead?arrow_forward
- This is Discreet math please answer questions with proper formatting for proofsarrow_forwardLet ƒ : Z → Z be some function over the integers. Select an appro- priate proof technique (direct, contradiction, induction, invariant or pigeonhole), and prove that if you have: a, f(a), ƒ(f(a)), ƒ(f(f(a))) and f(f(f(f(@)))), then at least 2 of those numbers are equivalent modulo 4.arrow_forwardMake a truth table for the following expression [8]:(a) ¬[(¬p −→ q) ∨ (¬p ∧ ¬q)] (b) Based on your truth table, classify the above expressionarrow_forward
- Prove by an appropriate reduction that the following set is not recursively enumerable: {⟨M⟩|M(⟨M⟩) ↑}, where ⟨M⟩ is the encoding of M.arrow_forward2arrow_forwardBig-Oh. For each function f in the left column of the following table,choose one expression O(g) from the following list:O(1/n),O(1),O(log2 n),O(n),O(n log2 n),O(n2),O(n10),O(2n),O(10n),O(nn)such that f ∈ O(g). Use each expression only once.arrow_forward
- Correct answer will be upvoted else downvoted. Computer science. You are given two integers n and k. You ought to make a variety of n positive integers a1,a2,… ,a to such an extent that the total (a1+a2+⋯+an) is distinguishable by k and greatest component in an is least conceivable. What is the base conceivable most extreme component in a? Input The primary line contains a solitary integer t (1≤t≤1000) — the number of experiments. The solitary line of each experiment contains two integers n and k (1≤n≤109; 1≤k≤109). Output For each experiment, print one integer — the base conceivable most extreme component in cluster a to such an extent that the aggregate (a1+⋯+an) is distinct by k.arrow_forwardLet f(n) and g(n) be positive functions over the natural numbers. For each of the following claims either prove formally that the claim is correct, or disprove it by giving a counter example. a) f(n) is e(f(n/2)) . b) f(n) + g(n) is E(min(f(n),g(n)). c) f(n) + g(n) is E(max(f(n),g(n)). d) if f(n)f(n) is O(n“) then f(n) is O(n).arrow_forwardProve that the sum of the first n odd positive integers is n2. In other words, show that 1 + 3 + 5 + .... + (2n + 1) = (n + 1)2 for all n ∈ N.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON
Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science
Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning 
Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning
Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education
Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY
Computer Networking: A Top-Down Approach (7th Edi...
Computer Engineering
ISBN:9780133594140
Author:James Kurose, Keith Ross
Publisher:PEARSON
Computer Organization and Design MIPS Edition, Fi...
Computer Engineering
ISBN:9780124077263
Author:David A. Patterson, John L. Hennessy
Publisher:Elsevier Science
Network+ Guide to Networks (MindTap Course List)
Computer Engineering
ISBN:9781337569330
Author:Jill West, Tamara Dean, Jean Andrews
Publisher:Cengage Learning
Concepts of Database Management
Computer Engineering
ISBN:9781337093422
Author:Joy L. Starks, Philip J. Pratt, Mary Z. Last
Publisher:Cengage Learning
Prelude to Programming
Computer Engineering
ISBN:9780133750423
Author:VENIT, Stewart
Publisher:Pearson Education
Sc Business Data Communications and Networking, T...
Computer Engineering
ISBN:9781119368830
Author:FITZGERALD
Publisher:WILEY