A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Related questions
Question
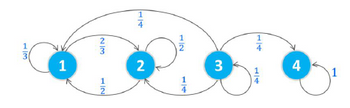
a.Here is the Markov Chain, then :
Which state is communicating?
Which are the transient states?
The systems are ergodic or non-ergodic?
b Explain reneging, balking, and jockeying in queueing theory!
c. Please pay attention to the following statements!
Statement 1: In making rational decisions, a player needs anticipation of the competitor’s response.
Statement 2: Competitor’s behavior can be expected.
Are the two above statements true or false?
Transcribed Image Text:فر البا
C
1
ده است
12
**
2
3
**
4
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step 1: Write the given information
VIEW Step 2: Determine the states which are communicating, transient and the check the systems are ergodic or not
VIEW Step 3: Explain reneging, balking, and jockeying in queueing theory
VIEW Step 4: Determine whether the given two statements are true or false
VIEW Solution
VIEW 
Step by stepSolved in 5 steps with 2 images
Knowledge Booster
Similar questions
- TOPIC: MARKOV CHAINS A housewife always uses one of three brands of detergent: "A", "B" or "C". Which one she buys depends inwhich of the three manufacturers is running a promotional campaign (with gifts such as combs, ornaments, etc.),etc.). Companies undertake such campaigns at random, regardless of whether or not competitors are running other campaigns at the same time.not running other campaigns at the same time. Brand "A" company runs a campaign ½ of the time, brand "B" runs a campaign 1/3 of the time, and brand "B" runs a campaign 1/3 of the time, and brand "C" runs a campaign 1/3 of the time.1/3 of the time, and "C" promotes 1/3 of the time. If the lady buys brand "A" on a certain occasion, the next time she will also buy brand "A".If she buys brand "A" on a certain occasion, the next time she will also buy brand "A", if your company is promoting or if neither of the other two is doing so.or she buys brand "B" if it is on promotion, but brand "A" is not, or she buys brand "C" if…arrow_forwardShow full answers and steps to part d) and e) using Markov Chain Theory. Please explain how you get to the answers without using excel, R or stataarrow_forwardThe Tiger Sports Shop1 has hired you as an analyst to understand its market position with respect to Clemson merchandise. It is particularly concerned about its major competitor, Mr. Knickerbocker, and which Clemson-related store has the ‘lead’ market share. Recent history has suggested that which Clemson-related store has the ‘lead market share’ can be modeled as a Markov Chain using three states: TSS (Tiger Sports Shop), MK (Mr. Knickerbocker), and Other Company (OC). Data on the lead market share is taken monthly and you have constructed the following one-step transition probability matrix from past data in the picture. a) The current state of the lead market share in October is that Tiger Sports Shop is in the lead (i.e., the Markov Chain in October is TSS). Tiger Sports Shop is considering launching a new brand in February only if it has the lead market share in January. Determine the probability that TSS will launch this new brand. Please show any equations or matrices…arrow_forward
- 1. Two risk neutral players compete to win a prize, P. The probability of winning depends on effort; the probability that player i wins equals e(e++e2), where ei is the effort level of player i. The cost of effort is ciei. a) Find the Nash equilibrium effort levels. b) What is the probability player 1 wins at equilibrium?arrow_forwardne bets $1. 0.45, he wins the game and with probability 1 - p = 0.55, he loses the game. His goal is to increase his capital to $3, and as soon as he does, the game is over. The game is also over if his capital is reduced to zero. Construct an absorbing Markov chain and answer the following questions. • What is the expected duration of the game? • What is the probability that he goes broke?arrow_forwardThe main topic is Markov Chains:Students in Geology class never know what is going to happen in the class, as the teacher may: give them a pop quiz, take them to field practice, analyze the topic of the day, or lecture on a special topic.If one day there is a test, the next day there is always a field practice.If one day there is field practice, the next day there is no practice or test, but there is still a chance of the day's topic or special lecture.of the day or of the special lecture.If on a certain day the topic is tested, the probabilities for the next day are ¼ for the test, 1/6 for the topic and 1/3 for the lecture.and 1/3 for the lecture.If one day there is a lecture, the odds for the next day are ¼ for the test, 1/8 for the practice, 1/8 for the topic analysis and ½ for the lecture.for the analysis of the topic and ½ for the lecture.One of the students has calculated that they can expect quizzes 43/287 of the lecture days; field practice72/287 of the class days; topic…arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
A First Course in Probability (10th Edition)
Probability
ISBN:9780134753119
Author:Sheldon Ross
Publisher:PEARSON