
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Question
HELP I NEED IN ONE HOUR.
I NEED PART B
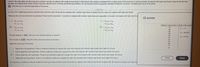
Transcribed Image Text:Listed in the data table are IQ scores for a random sample of subjects with medium lead levels in their blood. Also listed are statistics from a study done of IQ scores for a random sample of subjects with high lead levels. Assume that the two
samples are independent simple random samples selected from normally distributed populations. Do not assume that the population standard deviations are equal. Complete parts (a) and (b) below.
Click the icon to view the data table of IQ scores.
a. Use a 0.01 significance level to test the claim that the mean IQ scores for subjects with medium lead levels is higher than the mean for subjects with high lead levels.
What are the null and alternative hypotheses? Assume that population 1 consists of subjects with medium lead levels and population 2 consists of subjects with high lead leve
IQ scores
O A. Ho: H1 #H2
OB. Ho: H1= H2
H H1H2
Medium Lead Level High Lead Level
C. Ho: H1 SH2
o Ho H1 H2
H: Hy>Hz
72
n2 = 11
96
H:H>H2
92
X2 = 89.003
%3D
85
The test statistic is 0.41. (Round to two decimal places as needed.)
84
S2 = 9.752
97
The P-value is 0.343 (Round to three decimal places as needed.)
83
92
State the conclusion for the test.
95
111
91
O A. Reject the null hypothesis. There is sufficient evidence to support the claim that subjects with medium lead levels have higher IQ scores.
O B. Fail to reject the null hypothesis. There is sufficient evidence to support the claim that subjects with medium lead levels have higher IQ scores.
C. Fail to reject the null hypothesis. There is not sufficient evidence to support the claim that subjects with medium lead levels have higher IQ scores.
O D. Reject the null hypothesis. There is not sufficient evidence to support the claim that subjects with medium lead levels have higher IQ scores,
Print
Done
b. Construct a confidence interval suitable for testing the claim that the mean IQ scores for subjects with medium lead levels is higher than the mean for subjects with high lea
_

Transcribed Image Text:Listed in the data table are IQ scores for a random sample of subjects with medium lead levels in their blood. Also listed are statistics from a study done of IQ scores for a random sample of subied
samples are independent simple random samples selected from normally distributed populations. Do not assume that the population standard deviations are equal. Complete parts (a) and (b) belo
E Click the icon to view the data table of IQ scores.
VVI IJI YE VI JUI
O A Ho Hy # H2
O B. Ho P1 = P2
c.
. Ho H1 SH2
D. Ho: -H2
H: > P2
The test statistic is 0.41. (Round to two decimal places as needed.)
The P-value is 0.343. (Round to three decimal places as needed.)
State the conclusion for the test.
OA Reject the null hypothesis. There is sufficient evidence to support the claim that subjects with medium lead levels have higher IQ scores.
OB. Fail to reject the null hypothesis. There is sufficient evidence to support the claim that subjects with medium lead levels have higher IQ scores.
c. Fail to reject the null hypothesis. There is not sufficient evidence to support the claim that subjects with medium lead levels have higher IQ scores.
OD. Reject the null hypothesis. There is not sufficient evidence to support the claim that subjects with medium lead levels have higher IQ scores.
b. Construct a confidence interval suitable for testing the claim that the mean IQ scores for subjects with medium lead levels is higher than the mean for subjects with high lead levels.
(Round to two decimal places as needed.)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman