Question
Transcribed Image Text:### Rotation Dynamics - Problem 3
**Problem Statement:**
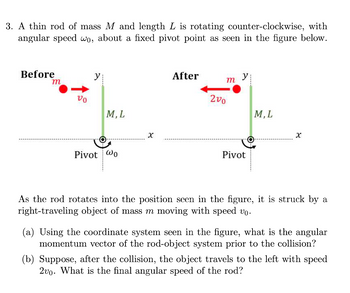
A thin rod of mass \( M \) and length \( L \) is rotating counter-clockwise, with angular speed \( \omega_0 \), about a fixed pivot point as seen in the figure below.
#### Diagram Description:
- **Before Collision:**
The rod is positioned vertically along the y-axis. The system is described as follows:
- Mass \( m \) is an object moving to the right with a speed \( v_0 \).
- The rotation pivot is at the origin of the coordinate system (0,0).
- The rod's angular speed is \( \omega_0 \).
- **After Collision:**
- The mass \( m \) travels to the left with a speed \( 2v_0 \) after collision.
- The rod and its specifications (mass \( M \), length \( L \)) remain the same.
#### Questions:
(a) Using the coordinate system seen in the figure, what is the angular momentum vector of the rod-object system prior to the collision?
(b) Suppose, after the collision, the object travels to the left with speed \( 2v_0 \). What is the final angular speed of the rod?
#### Solution Overview:
- **Angular Momentum Analysis before Collision:**
- Consider contributions from both the rotating rod and the moving mass \( m \).
- **Angular Momentum Conservation:**
- Apply conservation principles to ascertain the final angular speed of the rod after the collision.
### Detailed Solution:
#### (a) Angular Momentum before Collision
The angular momentum \( \vec{L}_{\text{initial}} \) of the system before the collision is the sum of the angular momentum of the rod and the angular momentum of the object \( m \).
1. **Rod (Rotating about Pivot):**
- Moment of inertia \( I_{\text{rod}} = \frac{1}{3}ML^2 \)
- Angular momentum \( \vec{L}_{\text{rod}} = I_{\text{rod}} \cdot \omega_0 = \frac{1}{3}ML^2 \omega_0 \)
2. **Object \( m \) (Moving with speed \( v_0 \)):**
- Position vector \( \vec{r} = L \hat{i} \) (since it's moving along the x-axis)
- Linear
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- A projectile of mass m moves to the right with a speed vi (see figure below). The projectile strikes and sticks to the end of a stationary rod of mass M, length d, pivoted about a frictionless axle perpendicular to the page through O. We wish to find the fractional change of kinetic energy in the system due to the collision. The moment of inertia of a rod is I = Md² and the moment of inertia of a particle is I = mr². 12 a. What is w, the angular speed of the system after the collision. mdvi Md²+1md² 12 b. What is the kinetic energy before the collision? Answer: KE¡ = m(v¡)². c. What is the kinetic energy after the collision? (0₁)² Answer: W= 1 m²d² Answer: KE₁ = = =+M₁2² +² md² 12 4 m O d M O 3arrow_forwardAs shown in the figure below, we have a square one meter on a side that is free to rotate about an axis perpendicular to the plane of the square, a distance a from one side and a distance b from the other side. a = b = b (i) Two forces, and F2, are applied to diagonally opposite corners, and act along the sides of the square, first as shown in case (i) and then as shown in case (ii) of the drawing. In each case the net torque produced by the forces is zero. If the magnitude of F2 is 4 times that of F₁, find the distances a and b that locate the axis. It should be noted that a and b are not drawn to scale. m m b aarrow_forwardIf small particle 'm' is placed a distance 'x' from the central axis of a solid disk of total mass M with 'r' radius, what would the be force?arrow_forward
arrow_back_ios
arrow_forward_ios