(a) the maximum vertical shear stress. (b) the maximum compression bending stress. (c) the maximum tension bending stress.

Question

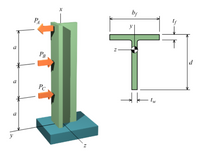
A cantilever beam supports the loads shown. The cross-sectional dimensions of the shape are also shown. Assume a = 0.6 m, P_A= 2.5 kN, P_B= 7.0 kN, P_C= 4.0 kN, d = 100 mm, b_f= 110 mm, t_f= 10 mm, t_w= 7 mm. Determine

(a) the maximum vertical shear stress.
(b) the maximum compression bending stress.
(c) the maximum tension bending stress.

See the coordinate system for the beam in the problem figure with the origin of the x axis at the fixed support. Consider four points along the beam’s axis:

Point A at x = 1.8 m
Point B at x = 1.2 m
Point C at x = 0.6 m
Point D at x = 0

Break the beam into three segments: AB, BC, and CD. Enter the shear force in each segment with its correct sign based on the coordinate system in the problem figure and the sign convention for shear forces in Chapter 7.

Answers:

V_AB =	kN
V_BC =	kN
V_CD =	kN

Enter the maximum shear force magnitude in the beam. Since this is a magnitude, enter a positive value.
Answer: V_max = kN

Enter the bending moment at four critical x-locations:
M_D is the moment at x = 0
M_C is the moment at x = 0.6 m
M_B is the moment at x = 1.2 m
M_A is the moment at x = 1.8 m
Enter each bending moment with its correct sign based on the coordinate system in the problem figure and the sign convention for bending moments presented in Chapter 7.
Answers:

M_A =	kN-m
M_B =	kN-m
M_C =	kN-m
M_D =	kN-m

Enter the maximum positive and negative bending moments for the beam. The “maximum negative bending moment” is the negative bending moment with the largest magnitude. Enter the maximum negative moment as a negative value here.
Answers:

M_{max, +} =	kN-m
M_{max, -} =	kN-m

Break the cross-sectional area into two areas:
(1) Top horizontal flange with rectangular cross-section 110 mm × 10 mm.
(2) Vertical stem with rectangular cross-section 7 mm × 90 mm.
Find the areas and the centroid locations in the y-direction for each area. Enter the centroid locations, y₁ and y₂, as measured with respect to a reference axis at the bottom of the cross-section. In other words, let y = 0 at the bottom edge of the vertical stem.
Answers:

A₁ =	mm²,	y₁ =	mm
A₂ =	mm²,	y₂ =	mm

Determine the centroid location in the y direction for the entire beam cross-section with respect to the reference axis at the bottom of the cross-section.

Answer: y¯ = mm

Consider again the cross-section broken into two areas, as in Step 1:
(1) Top horizontal flange with rectangular cross-section 110 mm × 10 mm.
(1) Top horizontal flange with rectangular cross-section 7 mm × 90 mm.
Determine the moment of inertia for each area about its own centroid and the distance from the centroid of each area to the centroid of the entire cross-section. For example, I_c₁ is the moment of inertia for area (1) about its own centroid, and d₁ is the distance from the centroid of area (1) to the centroid of the entire cross-section calculated in Step 6. Enter the distances d₁ and d₂ as positive values here, regardless of whether the centroid for an area is above or below the centroid of the entire cross-section.
Answers:

I_c₁ =	(10³) mm⁴,	d₁ =	mm
I_c₂ =	(10³) mm⁴,	d₂ =	mm

Calculate the moment of inertia for entire cross-section about its z centroidal axis.
Answer: I_z = (10⁶) mm⁴

Determine the maximum value of Q for the cross-section, where Q is the first moment of the area.
Answer: Q_max = (10³) mm³

Determine the maximum vertical shear stress.
Answer: τmax= MPa

At the location of the maximum positive moment, determine the maximum tension bending stress, σT+, and the maximum compression bending stress, σC+. Report the answers here using the correct signs according to the flexure formula (σC+ will be negative).
Answers:

σT+=	MPa
σC+	MPa

At the location of the maximum negative moment, determine the maximum tension bending stress, σT-, and the maximum compression bending stress, σC-. Report the answers here using the correct signs according to the flexure formula (σC- will be negative). Report these stresses in units of MPa.
Answers:

σT-=	MPa
σT-=	MPa

Determine the maximum compression bending stress at any location along the beam. This is the compression bending stress with the largest magnitude. Report the answer as a negative value to be consistent with the sign convention for normal stresses.
Answer: σC,max= MPa