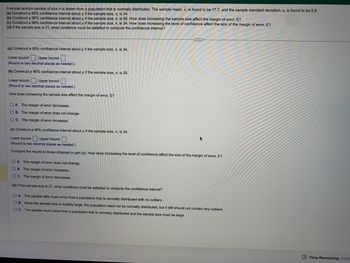
A simple random sample of size n is drawn from a population that is normally distributed. The sample mean, x, is found to be 17.7, and the sample standard deviation, s, is found to be 5.8. (a) Construct a 95% confidence interval about u if the sample size, n, is 34. (b) Construct a 95% confidence interval about µ if the sample size, n, is 55. How does increasing the sample size affect the margin of error, E? (c) Construct a 98% confidence interval about u if the sample size, n, is 34. How does increasing the level of confidence affect the size of the margin of error, E? (d) If the sample size is 21, what conditions must be satisfied to compute the confidence interval? (a) Construct a 95% confidence interval about u if the sample size, n, is 34. Lower bound:: Upper bound: (Round to two decimal places as needed.) (b) Construct a 95% confidence interval about u if the sample size, n, is 55. Lower bound:: Upper bound: (Round to two decimal places as needed.) How does increasing the sample size affect the margin of error, E? OA. The margin of error decreases. OB. The margin of error does not change. OC. The margin of error increases. HI (c) Construct a 98% confidence interval about u if the sample size, n, is 34. Lower bound:: Upper bound: (Round to two decimal places as needed.) Compare the results to those obtained in part (a). How does increasing the level of confidence affect the size of the margin of error, E? OA. The margin of error does not change. OB. The margin of error increases. OC. The margin of error decreases. (d) If the sample size is 21, what conditions must be satisfied to compute the confidence interval? OA. The sample data must come from a population that is normally distributed with no outliers. OB. Since the sample size is suitably large, the population need not be normally distributed, but it still should not contain any outliers. OC. The sample must come from a population that is normally distributed and the sample size must be large.

The provided information is as follows:The population is normally distributed.The sample mean is .The sample standard deviation is .a) The length of confidence is .The level of significance is calculated as follows:The sample size is .The degree of freedom is calculated as follows:The t-value is calculated as follows:The t-value is calculated using the Excel formula .The margin of error is calculated as follows:The 95% confidence interval is calculated as follows:The lower bound is 15.68, the upper bound is 19.72.b) The sample size is The degree of freedom is calculated as follows:The t-value is calculated as follows:.The t-value is calculated using the Excel formula .The margin of error is calculated as follows:The 95% confidence interval is calculated as follows:The lower bound is 16.13 and the upper bound is 19,27 when sample size is 55.As the sample size increases the margin of error decreases.Here the margin of error is 2.0237 when the sample size is 34 and the margin of error is 1.5680 when the sample size is 55.Option A is correct.The margin of error decreases.The length of the confidence interval is .The level of significance is calculated as follows:The sample size is 34.The degrees of freedom is calculated as follows:The t-value is calculated as follows:.The t-value is calculated using the Excel formula .c) The margin of error is calculated as follows:The 98% confidence interval is calculated as follows:The lower bound is 15.27 and the upper bound is 20.13 at 98% confidence level and the sample size is 34.The effect on the margin of error when the level of confidence increases is as follows:When the sample size is 34 and the level of confidence is 95% then the margin of error is 2.0237 and when the level of confidence is 98% at sample size 34 is 2.4318.Therefore, option B is correct.The margin of error increases.d) Option A is correct.The sample data must come from a population that is normally distributed with no outliers.Explanation :- Option A is correct because when computing a confidence interval, the normality assumption is crucial, especially for smaller sample sizes. In this case, the sample size is only 21, which is considered relatively small. Therefore, if the sample data does not come from a normally distributed population with no outliers, the confidence interval may not accurately reflect the true population parameter.Options B and C are incorrect.Option B is incorrect because even though a sample size of 21 might be considered moderately sized, it is not large enough to relax the assumption of normality. Generally, for smaller sample sizes, the normality assumption is crucial for the validity of confidence intervals.Option C is incorrect because while a normally distributed population is necessary for computing a confidence interval, the sample size does not necessarily have to be large. In fact, there are methods for computing confidence intervals for small samples sizes using non-parametric methods or bootstrapping techniques that do not rely on the normality assumption. However, these methods may have lower power or wider confidence intervals than traditional methods for large samples.a) The lower bound is 15.68, the upper bound is 19.72 when the sample size is 34.b) The lower bound is 16.13 and the upper bound is 19,27 when the sample size is 55.Option A is correct.The margin of error decreases.c) The lower bound is 15.27 and the upper bound is 20.13 at 98% confidence level and the sample size is 34.Option B is correct.The margin of error increases.d) Option A is correct.The sample data must come from a population that is normally distributed with no outliers.

Related questions