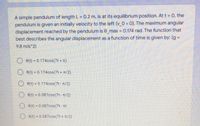
A simple pendulum of length L = 0.2 m, is at its equilibrium position. At t = 0, the pendulum is given an initially velocity to the left (v_0< 0). The maximum angular displacement reached by the pendulum is e_max = 0.174 rad. The function that best describes the angular displacement as a function of time is given by: (g = %3D %3D 9.8 m/s^2)

In the figure, a solid cylinder attached to a horizontal spring (k = 5.80 N/m) rolls without slipping along a horizontal surface. If the system is released from rest when the spring is stretched by 0.290 m, find (a) the translational kinetic energy and (b) the rotational kinetic energy of the cylinder as it passes through the equilibrium position. (c) If the cylinder has mass M = 6.20 kg, find the period of the simple harmonic motion that the cylinder's center of mass executes. (Hint: Find the time derivative of the total mechanical energy.) M · k oooooo (a) Number i 0. (b) Number i (c) Number i O. Units Units Units

You have made a physical pendulum by swinging a rod of mass M = 1.08 kg and length L = 1.45 meters around its end. The mass of the rod is distributed uniformly along its length. We will assume that the amplitude of the swing is max = 19.34 degrees. Solid Rod Swings in Simple Harmonic Motion ^ 0=-0, max 0=+0₁ max Determine all the following: The FORMULA for the moment of inertia of your rod, I = The distance from the pivot point to the Center-Of-Mass, d = The angular frequency of the pendulum, w = The amplitude of the motion in radians, max = radians The angular velocity when 0 = 64% of full swing, w(0 = 0.64 0max): NOTE: The first question requires a FORMULA, not a value. rad/sec = meters rad/sec

A simple pendulum comprised of a bob of mass  m = 172 g  and a lightweight string of length 76.0 cm is released from rest from an initial angle of 28.0° from the vertical. (a) Using the approach of simple harmonic motion, what is the maximum speed of the pendulum bob? m/s(b) Using the approach of simple harmonic motion, what is the maximum angular acceleration of the bob? rad/s2(c) How does the speed found in part (a) compare with that found by using a conservation of energy approach? (Assume that the values are nearly the same if within 10% of each other.) The speed is very different from that from part (a). The speed is nearly the same as that from part (a).