A rigid block of mass M is mounted on four elastic supports, as shown in the figure below. Asmall mass m drops from a heighth and adheres to the rigid block without rebounding, andthe spring constant of each elastic support is k. Determine the equation of motion of thesystem after the small mass strikes the block. Given the following values, if the equation ofmotion is in the form + ax = 0, determine the value of a.M = 55 kg; m = 6 kg; k=181 N/m; h = 20 cm The springs are modified, so that the equation of motion is now + 14 = 0. If x = 0 at thestatic equilibrium position when both masses are included, the initial position is given by. Hence, determine the initial velocity of the system at the point of impact,* (t = 0) = V₁ (units m/s).mg204kVo =If the resulting motion of the system after the impact is of the formr(t) = A cos wnt + B sin wnt, determine the values,A =B =wn (rad/s) =KkMmkx

A rigid block of mass M is mounted on four elastic supports, as shown in the figure below. A small mass m drops from a height hand adheres to the rigid block without rebounding, and the spring constant of each elastic support is k. Determine the equation of motion of the system after the small mass strikes the block. Given the following values, if the equation of motion is in the form + az = 0, determine the value of a. M = 55 kg; m = 6 kg; k=181 N/m; h= 20 cm

A rigid block of mass M is mounted on four elastic supports, as shown in the figure below. A small mass m drops from a height hand adheres to the rigid block without rebounding, and the spring constant of each elastic support is k. Determine the equation of motion of the system after the small mass strikes the block. Given the following values, if the equation of motion is in the form + az = 0, determine the value of a. M = 55 kg; m = 6 kg; k=181 N/m; h= 20 cm

Elements Of Electromagnetics

7th Edition

ISBN:9780190698614

Author:Sadiku, Matthew N. O.

Publisher:Sadiku, Matthew N. O.

ChapterMA: Math Assessment

Section: Chapter Questions

Problem 1.1MA

See similar textbooks

Related questions

Q: Q2. A spring with negligible mass and constant k is attached to one end to a block of mass m and…

A: We will try to approach this problem in work energy method

Q: 2. The figure below shows three points in the operation of the ballistic pendulum. The projectile…

A: In the given system, the pendulum is at rest and the ball is moving with an velocity vi towards the…

Q: A motor is using a pulley system to lift a block. The radius of pulley 1 is r₁= 500 mm, and the…

Q: The COF between 11 kg collar and shaft is 0.19. The spring is unstretched when s = 0 where it is…

A: Mass of the collar Coefficient of friction Spring constant, Initial velocity Height The spring is…

Q: The rope shown in the figure below is wound around a cylinder of mass 4.0 kg and I = 0.020 kg m2,…

Q: Two particles of same mass 'm' denoted by P₁ and P₂ are connected by a massless rod of length 'a'…

Q: Find the equations of motion for a lever of length 2a and of mass M rotating around its tip 8.₁ 20

A: The length of arm, L = 2aThe magnitude of mass = M

Q: Q Find the egquations of motion of the vi brating undamped system Lagrange method. Fig be low ,…

A: If the speed of masses m1 and m2 are x1˙ and x2˙ respectively then, The total kinetic energy of…

Q: The wheel is attached to the spring. The mass of the wheel is m=20 kg. The radius of the wheel is…

Q: 4. A helical spring has a stiffness 25000If a mass of 100kg is attached to its free end,pulled down…

A: Given data with suitable variables is shown below. k=25000 N/mm= 100 kgx0=50 mmr=30 mm It is…

Q: Plz solve correctly

A: Part (a): Finding the Speed of the 10-kg BlockInitially, the system is at rest, so the total…

Q: The thin rod in the figure has a mass of 15kg and is attached to a spring of constant k = 50 N / m…

A: Given: The mass of rod, m = 15 kg The spring stiffness, k = 50 N/m The unstretched length of spring,…

Q: 2) In figure, two blocks are connected by a massless string over a pulley of radius, 2R, and…

Q: A conservative mechanical system consists of a mass m that is constrained to move along a circle of…

A: Given: To find: Degree of freedom Lagrangian Euler-Lagrange equation

Q: find the equations of motion using the lagrange equations of motion. The main rod has length l and…

A: Given : To find : equation of motion

Q: Two springs and two masses are attached in a straight line on a horizontal frictionless surface as…

A: To determine the equation of motion of two mass systems given

Q: Find the minimum force P to start the motion of any part of the system of three blocks(Fig(3)).

Q: A pendulum consisting of a rod of mass 2m of mass 3kg and a ball of mass 1kg and a radius of 0.3m…

Q: A W = 58 lb block is pushed with a force that is defined by the equation F = (50+ s²) lb. The…

Q: When Crates A and B of mass mA = 37 kg and mB = 64 kg are released from rest, Crate A moves to the…

A: to determine - work done by the frictional force.

Q: A rigid block of mass M is mounted on four elastic supports, as shown in the figure below. A small…

A: Mass of the rigid block (M): M=55kgMass of the small dropped mass (m): m=6kgSpring constant of each…

Q: Problem 2: In the speed-governing mechanism m = 0.2kg. L = 10 cm (rods AB have negligible mass), w =…

Q: A homogeneous siender bar AB of mass m and length L is released from rest in the position shown i…

A: Given: A homogeneous Slender bar of length l and mass m is released from rest position as shown in…

Q: A spring is stretched 3 cm by a force of 6 N. Thus, according to Hooke's Law, the spring DO = 200 N.…

A: From the conservation of energy, the initial kinetic energy of the mass is equal to the final…

Q: DETAILS 1-11 Consider a frictionless track as shown in the figure below. A block of mass m₁ = 5.65…

Q: The figure shows a 5.50 kg block on a ramp. The block is also attached to a massless spring with…

Q: i. Your friend has chosen to use the rate form of the COLM to solve this problem. Neatly and…

Q: Find the equation of motion using the Lagrangian method? Problem 3.2 K1 wwwm K2 C www M2 O O F(t)…

A: we have lagrangian euation as ∂∂t∂L∂x·-∂L∂x=F(t)..............................(1)here L= Lagrangian…

Q: The collar of mass m = 77 kg in Figure Q14 slides outwards with an initial radial velocity vo = 0.58…

A: Given: The mass of the collar: →m=77 Kg Initial radial velocity of the collar: →vo=0.58 m/s…

Q: 2.1) A wheel with a mass and radius of gyration of 1.387 kg and 183 mm rolls down an incline as…

A: A) without friction fnet = mg sin (theta) a = r* angular acceleration

Q: In the system shown in the figure, the spring stiffness k = 2 × 103 N/m and the total massof the…

A: a) The free body diagram at the instant t, the mass system displaced x distance from the initial…

Q: By determining the equivalent spring constant of the mass spring system given in the figure, we…

A: Spring 1 and 2 are in parallel. The equivalent spring constant for parallel connection is, k12=k1+k2…

Q: The mechanism in the figure is in a vertical plane. Bar AC has a mass m, and the gravitational…

A: It is asked to find the reaction at 'A' and 'B' when the link OA rotates at constant angular…

Concept explainers

Forced undamped vibrations

In mechanical engineering, vibration is expressed as the term that occurs due to an object's backward and forward movement about a point of equilibrium. Generally, there are three types of vibrations which are,

Question

A rigid block of mass M is mounted on four elastic supports, as shown in the figure below. A
small mass m drops from a heighth and adheres to the rigid block without rebounding, and
the spring constant of each elastic support is k. Determine the equation of motion of the
system after the small mass strikes the block. Given the following values, if the equation of
motion is in the form + ax = 0, determine the value of a.
M = 55 kg; m = 6 kg; k=181 N/m; h = 20 cm

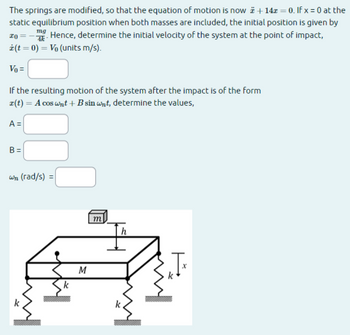
The springs are modified, so that the equation of motion is now + 14 = 0. If x = 0 at the
static equilibrium position when both masses are included, the initial position is given by
. Hence, determine the initial velocity of the system at the point of impact,
* (t = 0) = V₁ (units m/s).
mg
20
4k
Vo =
If the resulting motion of the system after the impact is of the form
r(t) = A cos wnt + B sin wnt, determine the values,
A =
B =
wn (rad/s) =
K
k
M
m
k
x

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

This is a popular solution!

SEE SOLUTION Check out a sample Q&A here

Step 1: Determine the given data

VIEW

Step 2: Calculate 'a'

VIEW

Step 3: Calculate the initial velocity

VIEW

Step 4: Solve the equation

VIEW

Solution

VIEW

Trending now

This is a popular solution!

Step by step

Solved in 5 steps with 18 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.

Similar questions

The thin rod in the figure has a mass of 15kg and is attached to a spring of constant k = 50 N / m at one end, which has an unstretched length of 1.5 m. If the rod is released from rest in horizontal position (e = 0 °) and only conservative forces act on it, determine: a) What is the moment of inertia of the thin rod around the axis of rotation at A? b) What is the angle at which the rod is momentarily at rest again? c) What is the maximum angular velocity of the path? 2 m 2 m ww. 60
33
find the equations of motion using the lagrange equations of motion. The main rod has length l and mass m, the left spring has spring constant k and right spring has spring constant 2k
1. Assuming the velocity of B=0.7 m/s after dropping 480 mm. Complete the following: a. Determine the spring constant such that all conditions mentioned above are met b. Using you value from part a, determine distacne B will drop if lowered slowly Notes: System is initially at rest Spring free length Cylinder mass - 25 kg Cylinder radius = 400 mm Ic cylinder 1.2 kg.m² 2 300 mm A Radius of pulley = 100 mm Ic value for pulley 0.5 kg.m² B10 kg Be
Mass of both blocks = 14kg. The friction coefficient for this bar is µ= 0.4. The spring constant k= 60 N/m. The spring is compressed 0.1 m and then released. d a Find: www 1. The magnitude of block B's acceleration 2. The magnitude of tension of the rope A B a=?
2. Derive the equation of motion for the system shown in the figure below using Newton-Euler method. K1 cm M, I cm M2 Inextensible K2
If both springs are usntretched when the mass is in the central position shown, determine the static deflection of the mass. What is the period of oscillatory motion about the position of static equilibrium? The mass m = 3.4, the spring constant k = 295 N/m, and the angle theta = 31 degrees
H4.
The thin rod of the figure has a mass of 15kg and is attached to a spring of constant K = 50 N/m at one end, which has an unstretched length of 1.5 m. If the rod is released from rest in horizontal position (ø = 0°) and only conservative forces act on it, determine: a) What is the moment of inertia of the thin rod around the axis of rotation in A? b) What is the angle at which the rod is momentarily resting again? c) What is the maximum angular speed of the route? Please attach the free body diagram if necessary. Thank you!
question in the figure
The mass m in the given figure is attached to a rigid lever with negligible mass and negligible friction in the pivot. The input is the displacement x. When x and θ are zero, the springs are at their free length. Assuming that θ is small, identify the equation of motion for θ with x as the input.
I need a clear and fast answer within 20 minutes. Thank you