
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question
Can you answer drop-down question on screenshot and questions G AND H
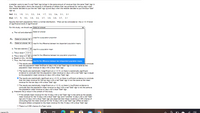
Transcribed Image Text:A retailer wants to see if a red "Sale" sign brings in the same amount of revenue than the same "Sale" sign in
blue. The data below shows the revenue in thousands of dollars that was achieved for various days when
the retailer decided to put the red "Sale" sign up and days when the retailer decided to put the blue "Sale"
sign up.
Red: 3.3,
1.9,
3.1,
2.3,
2.4,
1.7,
3.3,
2.6,
2.1,
2.1
Blue: 3.7,
5, 4.3,
3.4,
2.2,
3.7, 3.4,
2.4,
3.7, 3.1
Assume that both populations follow a normal distribution. What can be concluded at the a = 0.10 level
of significance level of significance?
For this study, we should use Select an answer
a. The null and alternativ Select an answer
z-test for a population proportion
Ho: Select an answer v
H: Select an answer vt-test for the difference between two dependent population means
b. The test statistic t Vt-test for a population mean
c. The p-value =0.0112
d. The p-value is > vaz-test for the difference between two population proportions
e. Based on this, we shoul
f. Thus, the final conclusi test for the difference between two independent population means
O The results are s
that the population mean revenue on days with a red "Sale" sign is not the same as the
population mean revenue on days with a blue "Sale" sign.
lo conclude
O The results are statistically insignificant at a = 0.10, so there is statistically significant
evidence to conclude that the population mean revenue on days with a red "Sale" sign is equal
to the population mean revenue on days with a blue "Sale" sign.
© The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude
that the mean revenue for the ten days with a red "Sale" sign is not the same as the mean
revenue for the ten days with a blue "Sale" sign.
O The results are statistically insignificant at a = 0.10, so there is insufficient evidence to
conclude that the population mean revenue on days with a red "Sale" sign is not the same as
the population mean revenue on days with a blue "Sale" sign.
g. Interpret the p-value in the context of the study.
Olf the sample mean revenue for the 10 days with a red "Sale" sign is the same as the sample
mean revenue for the 10 days with a blue "Sale" sign and if another 10 days with a red "Sale"
sign and 10 days with a blue "Sale" sign are observed then there would be a 0.58% chance of
concluding that the mean revenue for the 10 days with a red "Sale" sign differs at least 1
thousand dollars compared to the mean revenue for the 10 days with a blue "Sale" sign
O There is a 0.58% chance of a Type I error.
search
G M)

Transcribed Image Text:b. The test statistic t v = -3.174
(please show your answer to 3 decimal places.)
c. The p-value = 0.0112
d. The p-value is >va
e. Based on this, we should reject
f. Thus, the final conclusion is that ...
(Please show your answer to 4 decimal places.)
v the null hypothesis.
O The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude
that the population mean revenue on days with a red "Sale" sign is not the same as the
population mean revenue on days with a blue "Sale" sign.
O The results are statistically insignificant at a = 0.10, so there is statistically significant
evidence to conclude that the population mean revenue on days with a red "Sale" sign is equal
to the population mean revenue on days with a blue "Sale" sign.
O The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude
that the mean revenue for the ten days with a red "Sale" sign is not the same as the mean
revenue for the ten days with a blue "Sale" sign.
O The results are statistically insignificant at a = 0.10, so there is insufficient evidence to
conclude that the population mean revenue on days with a red "Sale" sign is not the same as
the population mean revenue on days with a blue "Sale" sign.
g. Interpret the p-value in the context of the study.
O If the sample mean revenue for the 10 days with a red "Sale" sign is the same as the sample
mean revenue for the 10 days with a blue "Sale" sign and if another 10 days with a red "Sale"
sign and 10 days with a blue "Sale" sign are observed then there would be a 0.58% chance of
concluding that the mean revenue for the 10 days with a red "Sale" sign differs at least 1
thousand dollars compared to the mean revenue for the 10 days with a blue "Sale" sign
O There is a 0.58% chance of a Type I error.
Olf the population mean revenue on days with a red "Sale" sign is the same as the population
mean revenue on days with a blue "Sale" sign and if another 10 days with a red "Sale" sign and
10 days with a blue "Sale" sign are observed then there would be a 0.58% chance that the mean
revenue for the 10 days with a red "Sale" sign would differ by at least 1 thousand dollars from
the mean revenue for the 10 days with a blue "Sale" sign
O There is a 0.58% chance that the mean revenue for the 10 days with a red "Sale" sign differs by
least 1 thousand dollars compared to the mean revenue for the 10 days with a blue "Sale" sign.
h. Interpret the level of significance in the context of the study.
O If the population mean revenue on days with a red "Sale" sign is the same as the population
mean revenue on days with a blue "Sale" sign and if another 10 days with a red "Sale" sign and
10 days with a blue "Sale" sign are observed then there would be a 10% chance that we would
end up falsely concluding that the population mean revenue for the days with a red "Sale" sign
is not the same as the population mean revenue on days with a blue "Sale" sign
O There is a 10% chance that there is a difference in the population mean revenue on days with a
red "Sale" sign and on days with a blue "Sale" sign.
O There is a 10% chance that green is your favorite color, so why woud you even consider red or
blue?
O f the population mean revenue on days with a red "Sale" sign is the same as the population
mean revenue on days with a blue "Sale" sign and if another 10 days with a red "Sale" sign and
10 days with a blue "Sale" sign are observed, then there would be a 10% chance that we would
end up falsely concluding that the sample mean revenue for these 10 days with a red "Sale"
sign and 10 days with a blue "Sale" sign differ from each other.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Since 1994, the Best Roller Coaster Poll has been ranking the world's roller coasters. In 2013, Bizarro dropped to 4th after eaming the top steel coaster rank for six straight years. Data on 11 of the top steel coasters from this poll are presented in the accompanying lable What do these data indicate about the Length of the track and the Duration of the ride you can expect? E Click the icon to view the steel coaster data. Construct a scatterplot of the data. Choose the correct plot below. A. OB. O D. Q 240 240 240- 240 40 2000 6000 Length (A) 40 2000 6000 2 40 2000 6000 (2 Length () 40 2000 Length () 6000 ( Length (n) Find the correlation coefficient. Steel coaster data (Round to three decimal places as Маx Max Vert Duration Height Speed (sec) Length (ft) Initial Angle Rank Roller Coaster (mph) (degrees) Park 1 Expedition GeForce Holiday Park Six Flags Kings Dominion SF New England Hersheypark Cedar Point PortAventua Six Flags Mirabilandia Location Drop (ft) (ft) DE 184 75 188 74.6 82…arrow_forwardwhat is domain and Range?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman