
Concept explainers
A population of values has a distribution with μ=127.7μ=127.7 and σ=10σ=10. You intend to draw a random
According to the Central Limit Theorem:
(a) What is the mean of the distribution of sample means?
μ¯x=μx¯=
(b) What is the standard deviation of the distribution of sample means?
(Report answer accurate to 2 decimal places.)
σ¯x=σx¯=
(c) In a random sample of n=103, what is the
(d) In a random sample of n=103, what is the probability that its sample mean is less than 128.5? Give your answer to three decimal places.
From the given information,
Mean = 127.7
Standard deviation = 10
Sample size = 103
a)
The mean of the distribution of sample means is,
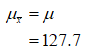
b)
The standard deviation of the distribution of sample means is,
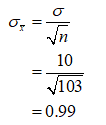
Step by stepSolved in 4 steps with 4 images

- A population of values has a normal distribution with μ=165.6μ=165.6 and σ=91.4σ=91.4. You intend to draw a random sample of size n=72n=72.What is the mean of the distribution of sample means?μ¯x=μx¯= What is the standard deviation of the distribution of sample means?σ¯x=σx¯= Round to 4 decimal places.arrow_forwardAssume the random variable X is normally distributed with mean μ=50 and standard deviation σ=7. Find the 87th percentile.arrow_forwardA research study investigated differences between male and female students. Based on the study results, we can assume the population mean and standard deviation for the GPA of male students are µ = 3.5 and σ = 0.5. Suppose a random sample of 100 male students is selected and the GPA for each student is calculated. Find the interval that contains 95.44 percent of the sample means for male students.arrow_forward
- A population has parameters μ=37μ=37 and σ=54.8σ=54.8. You intend to draw a random sample of size n=209n=209.What is the mean of the distribution of sample means?What is the standard deviation of the distribution of sample means?(Report answer accurate to 2 decimal places.)arrow_forwardA normal population has mean =μ9 and standard deviation =σ5 . Find the proportion of the population that is greater than 4 . Round the answers to at least four decimal places. The proportion of the population that is greater than 4 is .arrow_forwardK A population has a mean μ = 134 and a standard deviation o = 26. Find the mean and standard deviation of the sampling distribution of sample means with sample size n = 59. σ- The mean is μ- =, and the standard deviation is o- = (Round to three decimal places as needed.) X Z-arrow_forward
- (1 point) A random sample of 110 observations produced a mean of x = 34.7 from a population with a normal distribution and a standard deviation o = 4.39. (a) Find a 99% confidence interval for u (b) Find a 95% confidence interval for (c) Find a 90% confidence interval for uarrow_forwardThe temperature distribution of city D has a population mean µ= 21.3, and standard deviation o = 4.8. You randomly select 12 days and get the temperature for these days. Then you compute the sample mean. What is the maximum sample mean value in the bottom 0.22 x 100% of the sample mean distribution? Note that we're talking about the distribution of the sampling mean. Give your answer to 2 decimal places.arrow_forwardA person's blood glucose level and diabetes are closely related. Let x be a random variable measured in milligrams of glucose per deciliter (1/10 of a liter) of blood. Suppose that after a 12-hour fast, the random variable x will have a distribution that is approximately normal with mean μ = 88 and standard deviation σ = 21. Note: After 50 years of age, both the mean and standard deviation tend to increase. For an adult (under 50) after a 12-hour fast, find the following probabilities. (Round your answers to four decimal places.) (a) x is more than 60(b) x is less than 110(c) x is between 60 and 110(d) x is greater than 140 (borderline diabetes starts at 140)arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





