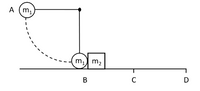
Question
A point mass m1 = 1.3 kg is attached to a massless rod with length L, so that together they form a simple pendulum. The pendulum is initially kept still in the horizontal position (A in the figure). On the surface below (B in the figure) lies a block at rest with mass m2 = 0.80 kg. This surface is frictionless between B and C, while there is friction between C and D (see figure). The distance between C and D is 0.30m. The air resistance is negligible in this task. The acceleration of gravity is given at g = 9.81 m / s.
The pendulum is now released so that it swings down. Immediately before m1 collides with m2, m1 has a velocity of 3.8 m / s.
- i) Draw a free-body diagram for m1 in the downswing as the angle between the pendulum and the vertical is 45◦.
- ii) Use the conservation of mechanical energy to find the length L of the pendulum (note that L is equal to the height from which the pendulum starts).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- This was rejected the first time. Can you please state why this is being rejected?arrow_forwardNote: Make sure your calculator is in radian mode for this problem, and that you switch it back after this problem. There are two particles (1 and 2) that are moving around in space. The force that particle 2 exerts on 1 is given by: F→21(t)=Fxe−(t/T)ı^+Fysin(2πt/T)ȷ^ Where the parameters have the values: Fx=14.2 N, Fy=89 N, T=55 s.We will consider a time interval that begins at ti=0 s and ends at tf=96 s. Find the x component of the impulse from 2 on 1 between ti and tf.arrow_forwardTwo pendula are shown in the figure. Each consists of a solid ball with uniform density and has a mass M. They are each suspended from the ceiling with massless rod as shown in the figure. The ball on the left pendulum is very small. The ball of the right pendulum has radius 1/2 L. L = 1.6 m Find the period T of the left pendulum for small displacements in s. Find the period T of the right pendulum for small displacements in s.arrow_forward
- The figure at right shows a pendulum consisting of a mass M = 2kg connected to a massless string of length L = 0.5m. The string is pulled back to an angle theta_0 = 20° and released from rest (V_0 = 0). What is the magnitude of the velocity v of the mass when the string returns to the vertical position (theta = 0°)?arrow_forwardH2. A simple pendulum has a particle of mass m at the end of a light rod of length 1. The other end of the rod is attached to a fixed point O, at the origin of polar coordinates (r, 0). The particle is at position (r, 0) with 0 = 0 corresponding to the particle being vertically below O. (a) Use the formulae for acceleration in polar coordinates, a = ( − rġ²) + (2rė + rö)ê to show that cos 0 + A, 8 T = mg cos 0 + mlė², where T' is the tension in the rod. Use the relation (0²) = 200 to deduce that 2g ². = 1 and 0 == sin sin 0, (1) where A is a constant. If the particle is instantaneously at rest ( = 0) when the rod is horizontal, find and T when the rod is vertical. How does the tension in the vertical position (which is also the maximal tension) depend on the rod's length /? (b) Assume the particle is subject to linear air resistance av. Use the expression of the velocity in polar coordinates v=rf+rẻÔ (2) together with (1) to write the equations of motion in polar coordinates. Show…arrow_forwardA mass m is attached to a spring of force constant 76.0 N/m and allowed to oscillate. The figure (Figure 1) shows a graph of its velocity vx as a function of time t. Find the period, frequency, and angular frequency of this motion. What is the amplitude (in cm)? At what times does the mass reach the position x=±A in the interval between t=0s and t=1.8s including the endpoints? Find the maximum acceleration of the mass. Find the times at which the maximum acceleration occurs in the interval between t=0s and t=1.8s including the endpoints. What is the mass m?arrow_forward
- A uniformly dense rigid rod with mass of 6 kg and length of 0.6 m rotates around its center of mass. Two springs with equal spring constants of 200 J/m2 are attached to each end of the rod (thus there are a total of four springs attached to the rod). What is the period (in s) of small amplitude oscillations of this system?arrow_forwardA cube, whose mass is 0.720 kg, is attached to a spring with a force constant of 110 N/m. The cube rests upon a frictionless, horizontal surface (shown in the figure below). A cube labeled m is attached to the right end of a horizontal spring, and the left end of the spring is attached to a wall. The spring is stretched horizontally such that the cube is displaced by a distance A to the right of its equilibrium position. The cube is pulled to the right a distance A = 0.140 m from its equilibrium position (the vertical dashed line) and held motionless. The cube is then released from rest. (a) At the instant of release, what is the magnitude of the spring force (in N) acting upon the cube? N (b) At that very instant, what is the magnitude of the cube's acceleration (in m/s2)? m/s2 (c) In what direction does the acceleration vector point at the instant of release? Away from the equilibrium position (i.e., to the right in the figure). Toward the equilibrium position (i.e., to…arrow_forward
arrow_back_ios
arrow_forward_ios