**Title: Exploring Simple Harmonic Motion (SHM) with Springs**In this physics lab activity, students are introduced to the principles of simple harmonic motion (SHM) by experimenting with a spring affixed to a horizontal support. The task involves calculating the spring constant, denoted as \( k \).**Experiment Procedure:**1. A mass of 255.0 g is suspended from the spring.2. This suspension causes the spring to displace by 47.5 cm from its original equilibrium position.**Objective 1: Calculate the Spring Constant**Using the provided displacement information, students will determine the spring constant (\( k \)).- **Spring Constant Formula:**\[\text{Spring Constant: } \_\_\_ \, \text{N/m}\]**Objective 2: Determine the Period of Oscillation**Once the spring is extended with the mass, it undergoes simple harmonic motion when displaced from its new equilibrium position. Students are tasked with calculating the period of oscillation (\( T \)), ignoring the mass of the spring itself.- **Period of Oscillation Formula:**\[T = \_\_\_ \, \text{s}\]Students will use the principles of SHM to complete these calculations, enhancing their understanding of dynamics and spring mechanics. In the final section of the lab, the student is asked to investigate the energy distribution of the spring system described previously. The student pulls the mass down an additional 35.6 cm from the equilibrium point of 47.5 cm when the mass is stationary and allows the system to oscillate. Using the equilibrium point of 47.5 cm as the zero point for total potential energy, calculate the velocity and total potential energy for each displacement given and insert the correct answer.| Displacement (cm) from equilibrium | Velocity (m/s) | Total potential energy (J) ||------------------------------------|----------------|----------------------------|| 35.6 | | || 26.1 | | |**Answer Bank:**- 1.62- 0.334- 1.10- 0.594- 0.180

Name: **Title: Exploring Simple Harmonic Motion (SHM) with Springs**In this
Uploaded: 2024-03-20T06:58:04.000Z
Channel: Bartleby
Description: **Title: Exploring Simple Harmonic Motion (SHM) with Springs**In this physics lab activity, students are introduced to the principles of simple harmonic motion (SHM) by experimenting with a spring affixed to a horizontal support. The task involves c

Hooke's law states that the restoring force applied by a spring is proportional to the displacement of the spring and opposite in direction. The energy of a particle in SHM changes periodically from P.E to K.E. Both potential and kinetic energy depends upon the square of the displacement.(1) From Hooke's law- ⇒F=kx⇒mg=kx⇒k=mgx⇒k=0.255 kg×9.8 m/s20.475 m⇒k=5.26 N/m (2) Time period of oscillation is given by-T=2πmk ⇒T=2π0.255 kg5.26 N/m⇒T=1.38 s (3) For displacement of 35.6 cm- Potential energy is given as-U=12kx2=12×5.26×(0.356)2 =0.334 J Since 35.6 cm is the maximum stretch from the equilibrium position, i.e., 47.5cm, so at 35.6cm all of the energy is in the form of potential energy. Kinetic energy is zero at this point.⇒Velocity at 35.6cm = 0 m/s So, total energy of the spring-mass system is 0.334 J. For displacement of 26.1cm- Potential energy is given as-U'=12kx'2=12×5.26×(0.261)2 =0.180 J Since total energy of the system is constant and is equal to 0.334 J Therefore, Kinetic energy at 26.1cm is given by-Total energy(T)=Kinetic energy (K')+potential energy (U')⇒K'=T-U'⇒K'=0.334 J-0.180 J⇒K'=0.154 J Now,∵K'=12mv'2⇒v'=2K'm⇒v'=2×0.154 0.255 kg⇒v'=1.10 m/s Conclusion: (1) Spring constant is 5.26 N/m(2) Time period of oscillation is 1.38 s(3) At 35.6cm velocity is zero and potential energy is 0.334 J At 26.1cm velocity is 1.10 m/s and potential energy is 0.180 J

Science

Physics

A physics lab is demonstrating the principles of simple harmonic motion (SHM) by using a spring affixed to a horizontal support. The student is asked to find the spring constant, k. After suspending a mass of 255.0 g from the spring, the student notices the spring is displaced 47.5 cm from its previous equilibrium. With this information, calculate the spring constant. spring constant: N/m When the spring, with the attached 255.0 g mass, is displaced from its new equilibrium position, it undergoes SHM. Calcula the period of oscillation, T, neglecting the mass of the spring itself.

A physics lab is demonstrating the principles of simple harmonic motion (SHM) by using a spring affixed to a horizontal support. The student is asked to find the spring constant, k. After suspending a mass of 255.0 g from the spring, the student notices the spring is displaced 47.5 cm from its previous equilibrium. With this information, calculate the spring constant. spring constant: N/m When the spring, with the attached 255.0 g mass, is displaced from its new equilibrium position, it undergoes SHM. Calcula the period of oscillation, T, neglecting the mass of the spring itself.

College Physics

11th Edition

ISBN:9781305952300

Author:Raymond A. Serway, Chris Vuille

Publisher:Raymond A. Serway, Chris Vuille

Chapter1: Units, Trigonometry. And Vectors

Section: Chapter Questions

Problem 1CQ: Estimate the order of magnitude of the length, in meters, of each of the following; (a) a mouse, (b)...

See similar textbooks

Related questions

Q: CALC Consider a spring that does not obey Hooke's law very faithfully. One end of the spring is…

A: We are aware that the force Fx=kx-bx2+cx3 operating along the x-axis with an x-component.K has a…

Q: To measure the static friction coefficient betwee

A: Given: Mass of the block is m=4.93kg Spring constant K=521 N/m compression x=0.0524m

Q: 2 - 250 mm -- 250 mm 350 mm 300 mm

A: Position 2, total length=350+250=600 mm Original length of the spring=250mm extended length of the…

Q: A spring with spring constant 94 N/m and rest length 27.2 cm is used to pull a wooden block of…

A: GIven data The spring constant is given as k = 94 N/m. The rest length is given as l = 27.2 cm. The…

Q: Under some circumstances when two parallel springs, with constants k1 and k2, support a single mass,…

A: Given data : Weighting W = 20 lb Spring elongation x1 = 8 inches x2 = 6 inches Downward…

Q: ungee jumper with mass 67.5 kg jumps from a high bridge. r arriving at his lowest point, he…

Q: A motionless block with mass m=11 kg is being pulled by a spring with a spring constant of k=35 N/m…

Q: A spring lies on a horizontal table, and the left end of the spring is attached to a wall. The other…

A: The spring can be stretched up to a distance of 0.073 m.Explanation:

Q: A mass of 0.83 kg is placed on a vertical spring. What is the spring constant, in N/m, of a…

Q: A 1.60 kg block slides on a rough horizontal surface. The block hits a spring with a speed of 2.10…

A: Given: m=1.60kgv=2.10 m/sx=11.0 cm=0.11mμ=0.460

Q: A 2.8 kg block is set on a horizontal table. One end of a spring is attached to the block, and the…

A: When block is released ,it will execute S.H.M. with Max elongation,A = 30 cm = 0.30 m . Mass of the…

Q: (a) Find the magnitude of the force required to compress the spring by 4.10 cm from its unstretched…

A: a) The spring force required to compressed by 4.10(x) cm from unstetched length, F= kx, where k=129…

Q: a spring hangs from the ceiling with an unstretched length of x0 = 0.87 m. A m1 = 7.1 kg block is…

A: Unstretched length of spring is Mass of object 1 is Stretched length due to object 1 is Mass of…

Q: m x=0 x = x₂ i (a) Find the speed the block has as it passes through equilibrium if the horizontal…

A: Mass(m) = 2 kg Expansion (xi)= 4.60 cm Spring constant (k) = 550 N/m

Q: A spring has a characteristic of k=7.50N/m. If the spring’s displacement is 0.550m from its…

A: The given values are,

Q: gy peno

A: Maximum kinetic energy of simple pendulum is KEmax = 1/2 m A2 w2 Angular frequency w= 2π /T m =…

Q: A 1.70-kg mass is attached to a vertical spring with spring constant, k=93.0 N/m and allowed to…

Q: Consider a system of two toy railway cars (i.e., frictionless masses) connected to each other by two…

A: Given Mass m1 = 4 kg Mass m2 = 2 kg Spring constant k1 = 32 N/m…

Q: The figure shows an approximate plot of stress (10° N/m2) versus strain for a thread that will break…

A: Stress versus strain graph is given for a thread. the stress is plotted along y axis and the strain…

Q: The springs of a pickup truck act like a single spring with a force constant of k = 1.05 × 105 N/m.…

Q: A spring that has stiffness constant 224N/m rests at its equilibrium length of 14cm, with one end…

A: Given : Stiffness constant (k) = 224 N/m Equilibrium length (L) = 14cm = 0.14 m Mass of a block (m)…

Q: A 10-kg block is attached to one end of a horizontal spring on a level, frictionless surface. The…

Q: A 15.0 kg crate is supported by a spring 1.) attached to the ceiling and a cable attached to the…

Q: A pen contains a spring with a spring constant of 240 N/m. When the tip of the pen is in its…

A: Given dataThe spring constant of the spring is: k = 240 N/mThe initial compression length of the…

Q: The springs of a pickup truck act like a single spring with a force constant of k = 1.15 × 105 N/m…

A: Given Spring constant is given as k=1.15×105 N/m Mass of the load is m=920 kg

Q: An object slides on a rough horizontal surface. It is attached to one end of a horizontal spring…

Q: A vertical spring is so that it's stretched 1/4 meter when a 1/2 kg mass is attached at the end of…

A: Given:mass attached to spring, m = 0.5 kgthe spring streches by d = 0.25 m to attain…

Q: The springs of a pickup truck act like a single spring with a force constant of 1.9×105 N/m1.9×105…

A: force constant = K = 1.9 x 105 N/m mass = m = 550 kg

Q: A mass of 2.24 kg is placed on a vertical spring. What is the spring constant, in N/m, of a…

Q: A 7.4-kg crate is attached to a horizontal spring with spring constant 900 N/m. You pull the crate…

A: Given: In this question, the given details are, A 7.4 kg crate is attached to a horizontal spring…

Q: Two identical springs, both of force constant k=200 N/m, are fixed at opposite ends of a level…

Q: A spring lies on a horizontal table, and the left end of the spring is attached to a wall. The other…

Q: 1. A 2.85-kg block compresses a spring (k-67.0 N/m) by 0.345 m from its equilibrium position. The…

Q: A mass resting on a horizontal, frictionless surface is attached to one end of a spring; the other…

A: Write the given values with the suitable variables. W=3 Jx=0.13 ma=12 m/s2 Here, W, x, and a are the…

Q: A 2.85 kgkg block on a horizontal floor is attached to a horizontal spring that is initially…

A: Apply Newton’s second law at the vertical motion of the block, then n-mg=0n=mg=2.85 kg9.8 m/s2=27.93…

Q: 10. A block with mass 0.50 kg is forced against a horizontal spring of negligible mass, compressing…

A: In the following question , when block is forced against horizontal spring it will loose some energy…

Q: 10. A block with mass 0.50 kg is forced against a horizontal spring of negligible mass, compressing…

Q: The cable OC and the springs OA and OB hold the 17 kg crate in static equilibrium. Both springs have…

Q: A block of mass 1.7 kg is attached to a horizontal spring that has a force constant 800 N/m as shown…

A: Here, m denotes the mass, k denotes the spring constant, xi denotes the initial compression, and F…

Concept explainers

Simple harmonic motion

Simple harmonic motion is a type of periodic motion in which an object undergoes oscillatory motion. The restoring force exerted by the object exhibiting SHM is proportional to the displacement from the equilibrium position. The force is directed towards the mean position. We see many examples of SHM around us, common ones are the motion of a pendulum, spring and vibration of strings in musical instruments, and so on.

Simple Pendulum

A simple pendulum comprises a heavy mass (called bob) attached to one end of the weightless and flexible string.

Oscillation

In Physics, oscillation means a repetitive motion that happens in a variation with respect to time. There is usually a central value, where the object would be at rest. Additionally, there are two or more positions between which the repetitive motion takes place. In mathematics, oscillations can also be described as vibrations. The most common examples of oscillation that is seen in daily lives include the alternating current (AC) or the motion of a moving pendulum.

Topic Video

Question

100%

**Title: Exploring Simple Harmonic Motion (SHM) with Springs**

In this physics lab activity, students are introduced to the principles of simple harmonic motion (SHM) by experimenting with a spring affixed to a horizontal support. The task involves calculating the spring constant, denoted as \( k \).

**Experiment Procedure:**

1. A mass of 255.0 g is suspended from the spring.
2. This suspension causes the spring to displace by 47.5 cm from its original equilibrium position.

**Objective 1: Calculate the Spring Constant**

Using the provided displacement information, students will determine the spring constant (\( k \)).

- **Spring Constant Formula:**

\[
\text{Spring Constant: } \_\_\_ \, \text{N/m}
\]

**Objective 2: Determine the Period of Oscillation**

Once the spring is extended with the mass, it undergoes simple harmonic motion when displaced from its new equilibrium position. Students are tasked with calculating the period of oscillation (\( T \)), ignoring the mass of the spring itself.

- **Period of Oscillation Formula:**

\[
T = \_\_\_ \, \text{s}
\]

Students will use the principles of SHM to complete these calculations, enhancing their understanding of dynamics and spring mechanics.

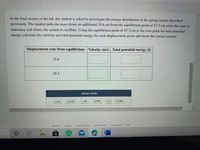
In the final section of the lab, the student is asked to investigate the energy distribution of the spring system described previously. The student pulls the mass down an additional 35.6 cm from the equilibrium point of 47.5 cm when the mass is stationary and allows the system to oscillate. Using the equilibrium point of 47.5 cm as the zero point for total potential energy, calculate the velocity and total potential energy for each displacement given and insert the correct answer.

| Displacement (cm) from equilibrium | Velocity (m/s) | Total potential energy (J) |
|------------------------------------|----------------|----------------------------|
| 35.6 | | |
| 26.1 | | |

**Answer Bank:**

- 1.62
- 0.334
- 1.10
- 0.594
- 0.180

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

This is a popular solution!

SEE SOLUTION Check out a sample Q&A here

Step 1

VIEW

Step 2

VIEW

Step 3

VIEW

Trending now

This is a popular solution!

Step by step

Solved in 3 steps

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.

Similar questions

The springs of a pickup truck act like a single spring with a force constant of k = 1.15 × 105 N/m. Part (a) How many centimeters will the truck be lowered by its maximum load of 960 kg? Part (b) If the pickup truck has four identical springs, what is the force constant of each, in newtons per meter? Assume the allowed compression is the same as in part (a).
A 4-kg object rests on a horizontal frictionless surface. It is in a position such that it is compressing a spring a distance 13.4 cm. If the object is released, the object leaves the spring at a speed of 19.6 cm/s. What is the spring constant of the spring? Express your answer in N/m, to at least one digit after the decimal point. plz use g = 9.8
A mass of 0.50 kg is held against compressed spring and released from rest while upon a horizontal, frictionless surface. The spring constant of the spring is 790 N/m and the mass leaves the spring with a speed of 7.84 m/s. Assume that the spring pushes the mass across the surface. By what amount was the spring initially compressed relative to its equilibrium position? 0.197
A vertical spring 0.100 meter long is stretched to a length of 1.25 meters when a 2 kilogram mass is attached to the bottom. What is the correct value for the spring constant of this spring?
A spring hangs vertically from a ceiling. The spring constant of the spring is k=15 N/m. A 2kg object has been attached to the spring and the spring has already come to its new equilibrium. Someone pulls the object down by 5cm and releases it at time t = 0s. The spring and object begin to oscillate under simple harmonic motion. Find the total energy of the system, the maximum kinetic energy, the maximum potential energy, and the positions where the maximum energies occur. Answers: 0.01875 J, 0.01875 J
An 8.00-kg block is attached to one end of a horizontal spring on a level, frictionless surface. The other end of the spring is attached to a vertical support. The spring obeys Hooke's law and has a spring constant of k =288 N/m. A physics student pulls the block outward so that the spring stretches by 50.0 cm. The student subsequently releases the block so that it undergoes simple harmonic motion. What is the maximum speed of the oscillator? a. 6.0 m/s b. 5.0 m/s c. 4.0 m/s d. 7.0 m/s e. 3.0 m/s
A mass resting on a horizontal, frictionless surface is attached to one end of a spring; the other end is fixed to a wall. It takes 3.1 J of work to compress the spring by 0.15 m . If the spring is compressed, and the mass is released from rest, it experiences a maximum acceleration of 12 m/s2. Find the value of the spring constant. Find the value of the mass.
A spring with spring constant 150 N/m and rest length 13.6 cm is used to pull a wooden block of weight 326 N horizontally across a tabletop at constant velocity. The coefficient of kinetic friction between the block and the table is 0.08, while the coefficient of static friction is 0.7. What is the length of the spring while it is pulling the block (in meters)?
A mass is oscillating with amplitude A at the end of the spring. How far is this mass from the equilibrium is the elastic potential energy equals y times the kinetic energy? Write the correct expression for the position æ in terms of the given variables. DO NOT use LaTeX codes when writing the expression. When typing Greek letters, just spell the name and DO NOT write backslashes, e.g. type alpha instead of \alpha. Answer: Display response
A 4.00 kg block is attached to a spring of force constant 500 N/m. The block is pulled 10.0 cm to the right of equilibrium and released from rest. Find the speed of the block as it passes through equilibrium if the coefficient of friction between block and surface is 0.250. Option1 Option2 Option3 Option4 Option5 0.542 m/s 0.675 m/s 0.765 m/s 0.871 m/s 0.986 m/s
A bungee jumper with mass 54.0 kg jumps from a high bridge. After arriving at his lowest point, he oscillates up and down, reaching a low point seven more times in 40.0 s . He finally comes to rest 21.0 m below the level of the bridge. Part A Estimate the spring stiffness constant of the bungee cord assuming SHM. k = Submit Part B lo = Submit MÅ Value 0 Request Answer Estimate the unstretched length of the bungee cord assuming SHM. µÅ Value Units Request Answer ? Units ?