Question
A particle of mass m in the figure below slides down a frictionless surface through height h and collides with a uniform vertical rod (of mass M and length d), sticking to it. The rod pivots about point O through an angle θ when it momentarily stops. Find θ in terms of m, M, g, h, d and various constants.
(Please type answer no write by hend)
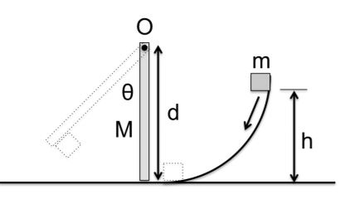
Transcribed Image Text:Ө
M
d
m
h
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
- As a torque activity, your Physics TA sets up the arrangement shown below. 3 fp = 8 F = 7₁ → A uniform rod of mass m, = 138 g and length L = 100.0 cm is attached to the wall with a pin as shown. Cords are attached to the rod at the r₁ = 10.0 cm and r₂ = 90.0 cm mark, passed over pulleys, and masses of m₁ = 266 g and m₂ = 157 g are attached. Your TA asks you to determine the following. (a) The position r3 on the rod where you would suspend a mass m3 = 200 g in order to balance the rod and keep it horizontal if released from a horizontal position. In addition, for this case, what force (magnitude and direction) does the pin exert the rod? Use standard angle notation to determine the direction of the force the pin exerts on the rod. Express the direction of the force the pin exerts on the rod as the angle 8, measured with respect to the positive x-axis (counterclockwise is positive and clockwise is negative). m4 Fp = 8 F = m N m₁ m₂ (b) Let's now remove the mass m3 and determine the new…arrow_forwardA bowling ball encounters a 0.760-m vertical rise on the way back to the ball rack, as the drawing illustrates. Ignore frictional losses and assume that the mass of the ball is distributed uniformly. The translational speed of the ball is 8.09 m/s at the bottom of the rise. Find the translational speed at the top. Number i Units 0.760 marrow_forwardPlease solve this correctlyarrow_forward
- In the figure, a small 0.176 kg block slides down a frictionless surface through height h = 0.427 m and then sticks to a uniform vertical rod of mass M = 0.352 kg and length d = 2.46 m. The rod pivots about point O through angle θ before momentarily stopping. Find θ.arrow_forwardA solid cylinder of mass m = 1kg, initially at rest, starts to roll down a rough surface inclined at a 300 angle to horizontal. The axis of the cylinder is attached through massless strings and pulleys to a square block of mass M = 2kg that rests initially on top of a horizontal table (see figure). What is the velocity of block M after the cylinder has traveled 1 m down the incline? The coefficient of kinetic friction between block M and the horizontal surface of the table is µ = 0.12. The cylinder rolls without slipping. M 0.37 m/s а. 2.50 m/s b. 1.62 m/s O c. 1.21 m/s O d. 1.43 m/s O e.arrow_forwardA ring (mass M) and disk (mass M) with radii R rotate in opposite directions.The ring rotates Clockwise with an angular speed 3ω, and the disk rotates Counterclockwise with a speed 2ωThe ring and the disk then "collide" and rotate together with the same ωf. What is the initial angular momentum of the ring. Remember, if the angular momentum is pointing down, it is negative, if it is pointing up it is positve.-3 MR2ω What is the initial angular momentum of the disk? Remember, if the angular momentum is pointing down, it is negative, if it is pointing up it is positve. What is the total angular momentum of the disk and ring together? What is the Moment of Inertia of the ring plus disk? What is the Angular velocity, ω of the ring plus disk after the collision?arrow_forward
- A thin- walled cylinder of radius 50 cm, mass 1.0 kg, is mounted on a frictionless, horizontal axle as in Figure 1 . A light cord wrapped around the wheel supports an object of mass 2 kg. When the wheel is released, the object accelerates downward, the cord unwraps off the wheel, and the wheel rotates with an angular acceleration. Find the angular acceleration of the wheel, , and the tension in the cord.arrow_forwardAt a certain instant, the particle of mass m has the position and velocity shown in the figure, and it is acted upon by the force F. Determine its angular momentum about point O and the time rate of change of this angular momentum. Use m = 1.9 kg, a = 0.62 m, b = 0.99 m, c = 0.72 m, and F = 190 N and v= 3.6 m/s. V Answers: j+ i k) kg m²/s Ho= Ho = j+ k) N•m i m C i+ i+ iarrow_forwardA disk of radius R=27 cm released from rest down a ramp. It rolls without slipping and its center of mass goes down by h=0.99 meters when it reaches the ground level. Find the center-of-mass speed of the disk right after it reaches the ground level. Enter your answer in m/s.arrow_forward
- A uniform plate of height 0.740 m is cut in the form of a parabolic section. The lower boundary of the plate is defined by: y= 1.100x^2 . Find the distance from the rounded tip of the plate to the center of mass. Needs Complete typed solution with 100 % accuracy.arrow_forwardChapter 11, Problem 066 GO Your answer is partially correct. Try again. In the figure, a small 0.109 kg block slides down a frictionless surface through height h = 1.46 m and then sticks to a uniform vertical rod of mass M = 0.218 kg and length d = 1.55 m. The rod pivots about point O through angle e before momentarily stopping. Find 0. Number Units (degrees) em the tolerance is +/-2% em Click if you would like to Show Work for this question: Open Show Workarrow_forwardA projectile of mass m moves to the right with a speed vi (see figure below). The projectile strikes and sticks to the end of a stationary rod of mass M, length d, pivoted about a frictionless axle perpendicular to the page through O. We wish to find the fractional change of kinetic energy in the system due to the collision. The moment of inertia of a rod is I = Md² and the moment of inertia of a particle is I = mr². 12 a. What is w, the angular speed of the system after the collision. mdvi Md²+1md² 12 b. What is the kinetic energy before the collision? Answer: KE¡ = m(v¡)². c. What is the kinetic energy after the collision? (0₁)² Answer: W= 1 m²d² Answer: KE₁ = = =+M₁2² +² md² 12 4 m O d M O 3arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios