Question
A light rigid rod of length ℓ = 1.00 m in length rotates about an axis perpendicular to its length and through its center, as shown in the figure below. Two particles of masses m1 = 4.80 kg and m2 = 3.00 kg are connected to the ends of the rod. What is the
______________ J s
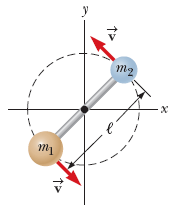
Transcribed Image Text:m1
TD
↑>
m₂
·x
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps

Knowledge Booster
Similar questions
- After all the metal has unwound from the roller, the student measures the radius R and the angular speed wo of the roller to be 25 cm and 20 rad/s respectively. Observed from the side, the roller rotates counterclockwise, as shown. A piece of clay of mass m strikes the very bottom edge of the roller with a horizontal velocity v = 4.0 m/s. The clay sticks to and rotates with the roller. The clay-roller system then rotates with a final angular velocity wi. (f) Is wi greater than, less than, or equal to wo? Justify your answer.arrow_forwardA bullet with mass of 25 grams traveling at speed of 185m/s hits the end of a rod as shown. The rod has a mass of 3 kg and a length of 80 cm, and it is free to spin about a perpendicular axis located at its center. If the bullet remains stuck in the end of the rod, what will be the angular speed of the rod after the bullet hits it? Let MM be the mass of the rod and mm be the mass of the bullet. The moment of inertia of a rod rotating about a perpendicular axis through its center is (1/12)ML2.(1/12)ML2. (Hint: After the bullet is embedded in the rod, it contributes m(L/2)2m(L/2)2to the moment of inertia of the rod.)arrow_forwardTwo disks are initially spinning, one above the other on a small axle that provides a small, but non-negligible torque from friction, as shown in the figure below. Both disks have the same radius, R = 2.58 m. Disk 1 has a moment of inertia I1 = 9.8 kg⋅m2. Disk 2 has a moment of inertia I2 = 5 kg⋅ m2. Let vertically up be the z direction, such that counterclockwise rotation as viewed from above corresponds to positive values of the z-component. Disk 1 is initially spinning with a z-component of angular velocity ω1,z = 21 rad/s, and disk 2 is initially spinning with a z-component of angular velocity ω2,z = -15 rad/s. Disk 1 is then dropped on disk 2, and the two discs quickly reach a common, final angular velocity. Find the z-component of their common angular velocity.arrow_forward
- A 10 kg wheel with a 0.4 meter radius is rotating at 4 rad/s. A 8 Nm torque is applied to the wheel. The rotational inertia of the wheel is 0.48 kgm2. The angular momentum of the wheel changes by 4 kg*m2/s. How long was the torque applied to the wheel. - 8 s - 3 s - 4 s - 0.5 sarrow_forwardAs shown in Figure , a 0.500 kg stone moving horizontally with a speed of 2.25 m/s collides with a 0.750 m long stationary vertical uniform rod. The rod has a mass of 1.50 kg and is fixed to the ground by a frictionless hinge. After the collision, the stone drops vertically down to the ground. What is the angular speed of the rod just after the collision? 0.25 m A) 2.00 rad/s B) 1.00 rad/s C) 3.00 rad/s D) 4.00 rad/s E) 5.00 rad/s stone v = 2.25 m/s 0.75 m Hingearrow_forwardA solid uniform spherical boulder travels down a hill. At the top of the hill the boulder is rolling with a horizontal speed of 5 m/s. The top half of the hill is rough, so that the boulder continues to roll without slipping. The bottom half of the hill and the valley is covered in smooth ice, so that there is no static friction between the boulder and the hill. How fast is the boulder moving when it gets to the bottom of the hill? What is its rotational speed in the valley if the boulder has a radius of 10 cm? Rough 50.0 m Smootharrow_forward
- A potter's disk spins from rest up to 3.8 rev/s in 15 s. The disk has a mass 3.5 kg and radius 24.0 cm. What is the angular momentum (in kg · m2/s) of the disk at t = 5 s? (Enter the magnitude.) What is the angular momentum (in kg · m2/s) of the disk at t = 10 s?(Enter the magnitude.)arrow_forwardEach of the following objects has a radius of 0.168 m and a mass of 2.67 kg, and each rotates about an axis through its center (as in this table) with an angular speed of 40.1 rad/s. Find the magnitude of the angular momentum of each object. a hoop a solid cylinder a solid sphere a hollow spherical shellarrow_forwardDetermine the angular momentum of a 78-g particle about the origin of coordinates when the particle is at x = 4.9 m, y = -6.3 m, and it has velocity v = (3.51-80k) m/s. Find the x-component. Express your answer using two significant figures. Lx = ΜΕ ΑΣΦ Submit Request Answer ▼ Part B Find the y-component. Express your answer using two significant figures. Ly= ΜΕ ΑΣΦ Submit Request Answer Part C Find the z-component. Express your answer using two significant figures. ? kg-m²/s ? kg-m²/sarrow_forward
- The figure shows three 0.0115 kg particles that have been glued to a rod of length L=5.79 cm and negligible mass. The assembly can rotate around a perpendicular axis through point O at the left end. If we remove one particle (that is, 33% of the mass), by what percentage does the rotational inertia of the assembly around the rotation axis decrease when that removed particle is the middle one?arrow_forwardChange in angular momentum. In the figure below, a Texas cockroach with mass m = 0.0470 kg (they are large) rides on a uniform disk of mass M = 10.8m and radius R = 0.0960 m. The disk rotates like a merry-go-round around its central axis. Initially, the cockroach is at radius r = R and the angular speed of the disk is w; = 0.910 rad/s. Treat the cockroach as a particle. The cockroach crawls inward to r = 0.330R. What is the change in angular momentum of (a) the cockroach-disk system, (b) the cockroach, and (c) the disk? (a) Number (b) Number (c) Number p. Units Units Units Rotation axis ◄►arrow_forwardA merry-go-round with a moment of inertia of 880kg⋅m2 experiences a force of 74.5N applied parallel to its edge, which is 3.35m from its axis of rotation. If the force lasts for 6.4s, what is the angular velocity of the merry-go-round, assuming it starts at rest? What is the angular momentum of the merry-go-round at this time?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios