Elements Of Electromagnetics
7th Edition
ISBN: 9780190698614
Author: Sadiku, Matthew N. O.
Publisher: Oxford University Press
expand_more
expand_more
format_list_bulleted
Related questions
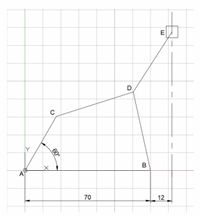
Concept explainers
Question
A four-bar
1.Draw the mechanism in appropriate scale on your paper
2. Find the instantaneous linear velocity of C
3. Find a point on your paper to draw the velocity polygon and scale the magnitude of the computed linear
velocity
4. Use the relative velocity equation for finding the linear
velocity of D; ? = ? + ?
? ? ?/?
5. Remember that although the magnitudes are unknown, their directions can be identified
6. Obtain the magnitudes of the unknown velocities from the velocity polygon
7. For Link DE, repeat the process by using ? = ? + ??
the line as much as needed
8. Remember that E is a SLIDER therefore it can only go
in the direction where its movement is not constrained
? . Add the
?/? ?/?
?
Transcribed Image Text:E
D
В
A
70
12
60°
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 1 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- P1 00:00 A 650.00 F 420.00 P B 450.00 P2 A four-bar mechanism is given in the below figure. Link P₁A and P₂B are made by steel and have uniform cross sections. The PAB section, which is a right triangle, made by aluminium. Link P₁A has rotational velocity and acceleration of 8 rad/s and 20 rad/s² (both counterclockwise), respectively. There is a horizontal force at P of F= 200 N. Given G₂, G3 and G4 are the centre of mass of the links P₁A, PAB and P₂B, respectively. The masses of the links P₁A, PAB and P₂B are in turn m₂ = 1 kg: m3 = 2 kg and m4 = 1.2 kg. The moment of inertia of the links P1A, PAB and P₂B are in turn IG2 = 0.08 kgm²; IG3 = 0.15 kgm² and IG4 = 0.1 kgm². Find all the forces acting on the joints at this instant.arrow_forwardPlease make sure to change the angle BCD to 45 degrees before solving! The picture is wrong. Thank you!!arrow_forwardFind the magnatidue of VB(ft/s): Find the angle of VB(degrees)arrow_forward
- q4arrow_forwardHello, I'm having difficulty undertanding this kinematics equation. A step by step answer would be appreciated. Thank you.arrow_forwardGiven: The link is connected to a collar which slides along bar AC. AC rotates with vector_ »AC= 3k (rad/s), vector_aAC= 2.4k (rad/s^2) A WAC, (AC ф- 55° 0= 25° Length of link BD= 0.2m, AB= 1.5m Find: D B The magnitude of the angular velocity of link BD The magnitude of angular acceleration of link BD. The relative acceleration of collar B.arrow_forward
- Given: A shaft rotates about a fixed vertical axis at a constant rate of f, as shown below. A straight bar OA, having a length of L, is pinned to point O on the shaft, with O being on the rotation axis of the shaft. At the instant when 80, bar OA is being raised at a rate of 6 from the horizontal plane, with this rate changing at a rate of . A set of ryz coordinate axes is attached to bar OA with its origin at O. A second set of coordinate axes, XYZ, are fixed to ground. At the instant when = 0, the zyz and XYZ axes are aligned with each other. Find: For the instant when -0°, determine the angular velocity and angular acceleration of har OA. vertical shaft bearing O 8 X bar Use the following parameters in your analysis: f2=5 rad/s, é = 4 rad/s, 6-3 rad/s² and L=2 m.arrow_forward1 of 1 3. A four-bar linkage is shown below. (A) the directions of each. (B) E on link 3. Use the method of velocity vector polygons to calculate w, and wq. Report Find and report the magnitude and direction of the absolute velocity of point RAD = 10 cm, Rap = 15 cm, Ra = 60 cm; R = 65 cm; Rp = 15 cm W2 = 2 rad/s cw (Note: ADB and FEC are right triangles.) link 3 A. link 2arrow_forwardFor the mechanism shown below, use the graphical position analysis to specify the value(s) of 02 when the linear speed of link 6 is zero. The parameters of each link length is: L2 = 3 cm, L3 =10 cm (O₂B), L5 = 4 cm, L σ₂³ = 5 cm. ////////////////// 5 B 4 0₂ 2 3 A₂ on 2 and 4 A3 on 3 10.5 cmarrow_forward
- Find the acceleration of the specified object. (Hint: Recall that if a variable is changing at a constant rate, its acceleration is zero.) A boat is pulled into a dock by means of a winch 16 feet above the deck of the boat (see figure). The winch pulls in rope at a rate of 7 feet per second. Find the acceleration of the boat when there is a total of 20 feet of rope out. (Round your answer to three decimal places.) ft/sec² Need Help? Read It Not drawn to scalearrow_forwardThe figure shows a closed-loop mechanism in which link AB of length 1m rotates about a fixed point at A. A second link BC, of length 3m, is pivoted to AB at B; the other end C is constrained to move in a fixed slot which in angled at 45 degrees to the horizontal. At the instance shown, AB is at 60 degrees to the horizontal, and rotating anticlockwise at 5 rad/s. At this instance, in what direction is the link BC rotating? You may wish to sketch a rough velocity vector diagram for this closed loop mechanism to assist you. WAB = 5 rad/s O O O O O Don't Know Anticlockwise B Rotating out-of-plane No rotation Clockwise 60⁰ BL 45⁰arrow_forwardWhat would be the Direction Cosine Matrix if there was a rotation about q for 120 degrees. I know that q would be lambda and theta = 120 degrees. But we don't have any measure numbers for lambda, so I can't create a DCM using Principle Rotation Parameters. Would you do it using the Euler Angles method? If so, how?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education 
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY