Practical Management Science
6th Edition
ISBN: 9781337406659
Author: WINSTON, Wayne L.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Related questions
Question
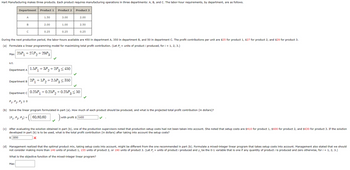
Transcribed Image Text:Hart Manufacturing makes three products. Each product requires manufacturing operations in three departments: A, B, and C. The labor-hour requirements, by department, are as follows.
s.t.
Department Product 1
A
B
с
1.50
Max
2.00
0.25
Product 2 Product 3
3.00
1.00
0.25
Department A 1.5P₁+3P₂ +2P3 ≤ 450
Department B2P₁ + 1P₂ +2.5P3 ≤ 350
Department c 0.25P₁ +0.25P₂ +0.25P3 ≤ 50
P1 P₂ P3 20
2.00
During the next production period, the labor-hours available are 450 in department A, 350 in department B, and 50 in department C. The profit contributions per unit are $25 for product 1, $27 for product 2, and $29 for product 3.
(a) Formulate a linear programming model for maximizing total profit contribution. (Let P; = units of product produced, for i = 1, 2, 3.)
Max 25P₁ +27P2+29P3
2.50
0.25
(b) Solve the linear program formulated in part (a). How much of each product should be produced, and what is the projected total profit contribution (in dollars)?
(P₁, P₂, P3) =
60,80,60
with profit $ 5400
(c) After evaluating the solution obtained in part (b), one of the production supervisors noted that production setup costs had not been taken into account. She noted that setup costs are $410 for product 1, $600 for product 2, and $630 for product 3. If the solution
developed in part (b) is to be used, what is the total profit contribution (in dollars) after taking into account the setup costs?
$3890
X
(d) Management realized that the optimal product mix, taking setup costs into account, might be different from the one recommended in part (b). Formulate a mixed-integer linear program that takes setup costs into account. Management also stated that we should
not consider making more than 140 units of product 1, 155 units of product 2, or 190 units of product 3. (Let P, = units of product i produced and y, be the 0-1 variable that is one if any quantity of product i is produced and zero otherwise, for i = 1, 2, 3.)
What is the objective function of the mixed-integer linear program?
Transcribed Image Text:In addition to the constraints from part (a), what other constraints should be added to the mixed-integer linear program?
s.t.
units of Product 1 produced
units of Product 2 produced
units of Product 3 produced
P₁ P₂ P3 2 0; Y₁ Y₂Y3 = 0, 1
(e) Solve the mixed-integer linear program formulated in part (d). How much of each product should be produced, and what is the projected total profit (in dollars) contribution?
= (C
1)
(P₁ P2 P3 Y₁1 Y2r Y 3) =
with profit $
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 6 steps with 11 images
Knowledge Booster
Similar questions
- Accompany makes two products (1&2) each product requires time on two machines (A&B). specification for each product is as follows. Product1 product2 Processing time on Machine A (hrs/unit) 2 2 Processing time on Machine B (hrs/unit) 1 2 Material and labour cost ( ksh/unit) 14 15 Selling price (ksh/unit) 16 18 Maximum possible sale (units) 130 150 The amount of time available on machine A is 360 hours and on machine B is 260 hours. Formulate the linear programme which, when…arrow_forward#4- The mean number of air conditioning units assembled per month by Freeze, Inc. is 750 and the standard deviation is 100 units. a. If the number of air conditioning units assembled per month follows a normal distribution, calculate the probability of Freeze, Inc to assemble a quantity of air conditioning units greater than the monthly break-even point calculated in problem 3-a. b. An improved assembling process is proposed to Freeze, Inc. to reduce the variable cost from $500 per unit to $400 per unit., increase the mean number of air conditioning units assembled per month from 750 to 850 and reduce the standard deviation to 90 units. As a result of the improvements, monthly fixed costs would go up from $250,000 to $300,000. Once these improvements are implemented, calculate the new number of air conditioning units that Freeze Inc. must sell every month to break-even, discuss and justify if you would recommend the process improvement initiative. c. If the number of air conditioning…arrow_forwardConsistently outperforming the market based on the technical analysis tends to: 1) support the semistrong form of the EMH. 2) not support the semistrong form of the EMH. 3) not support the weak form of the EMH. 4) support the weak form of the EMH.arrow_forward
- Bruce Corporation makes four products in a single facility. These products have the following unit product costs: Products Direct materials Direct labor Variable manufacturing overhead Fixed manufacturing overhead Unit product cost Additional data concerning these products are listed below. A B C $15.30 $ 11.20 $12.00 20.40 28.40 34.60 3.70 3.60 4.20 35.80 27.60 38.20 $79.10 $ 77.80 $ 95.40 5.30 27.50 $ 68.50 Multiple Choice A 4.80 $77.10 $ 3.20 5,000 D $11.60 41.40 Products C D 4.40 5.30 $88.40 $ 105.20 $ 4.30 $ 2.60 4,000 3,000 Grinding minutes per unit B 6.30 $ 94.50 $ 2.20 Selling price per unit Variable selling cost per unit Monthly demand in units 5,000 The grinding machines are potentially the constraint in the production facility. A total of 89,600 minutes are available per month on these machines. Direct labor is a variable cost in this company. Up to how much should the company be willing to pay for one additional minute of grinding machine time if the company has made the…arrow_forwardShoes Ltd. manufactures three items: Sneakers, Takkies and Sandals. The table below contains information regarding these products: Sneakers (R/ unit) Takkies (R/ unit) Sandals (R/ unit) Material cost 60 75 40 Labour cost 24 68 42 Variable overhead cost 7 12 16 Fixed overhead cost 36 23 11 Selling price per unit 870 990 650 Volume of production 12 000 28 500 31 200 Fixed overheads are allocated to products based on direct labour hours. Direct labour hours are constrained and therefore limited to 140 000 hours. The direct labour rate is R25 per hour. w Required: Q.3.1 Calculate the contribution margin per labour hour and then rank the products in order of profitability. Q.3.2 Calculate the number of units of each product that needs to be manufactured toarrow_forwardA bicycle component manufacturer produces hubs for bike wheels. Two processes are possible for manufacturing, and the parameters of each process are as follows: Process 1 Production rate Daily production time Process 2 35 parts/hour 4 hours/day 20% 15 parts/hour 7 hours/day 9% Percent parts rejected Assume that the daily demand for hubs allows all defect-free hubs to be sold. Select the process that maximizes profit per day if each part is made from $4 worth of material and can be sold for $30. Both processes are fully automated, and variable overhead cost is charged at the rate of $40 per hour.arrow_forward
- XYZ Leather Company manufactures and sells two products, wallets and belts, in its two-department plant. Operating data pertaining to the two products are as follows: Wallets Belts Selling price per unit P30 P50 Cost per unit: Variable manufacturing costs P8 P15 Variable marketing costs P2 P3 Fixed manufacturing costs P5 P5 Fixed marketing costs P6 P1 Cutting Finishing…arrow_forwardTuff-Rider, Inc., manufactures touring bikes and mountainbikes in a variety of frame sizes, colors, and component com-binations. Identical bicycles are produced in lots of 100. Theprojected demand, lot size, and time standards are shown inthe following table: Item Touring MountainDemand forecast 5,000 units/year 10,000 units/yearLot size 100 units 100 unitsStandard processing time .25 hour/unit .50 hour/unitStandard setup time 2 hours/lot 3 hours/lot The shop currently works 8 hours a day, 5 days a week,50 weeks a year. It operates five workstations, each producingone bicycle in the time shown in the table. The shop main-tains a 15 percent capacity cushion. How many workstationswill be required next year to meet expected demand withoutusing overtime and without decreasing the firm’s currentcapacity cushion?arrow_forwardeconomics of using mechaniz The following are the different phases in the analytical approach and process. Ind k. Establishment of budgetary c h Evaluation of the applicability Preparation of accounting syt d. The primary purpose of MAS is to improve the client firm's use of its capabal Exercise 2: Classification of Services and finance funetions: a Job evaluation and administration Industrial engineering e. Development of management-oriented accounting reporting system d Operations research e Investment management E Development of compensation programs g. Management or operations audit equipment i. and procedures manual i Revision of pension plans of 1. Marketing Cost reduction studies m. Exercise 3: Phases in the Analytical Approach and Process the sequence in which they are performed by writing the corresponding number of If it is not included, write NA. Advising and providing technical assistance in implementing recommendations Seeking and identifying objectives Evaluating and…arrow_forward
- What relationship between x and y is suggested by the scattergram? OA a quadratic relationship with downward concavity OB. a linear relationship with positive slope OC. a linear relationship with negative slope D. a quadratic relationship with upward concavityarrow_forwardSemans is a manufacturer that produces bracket assemblies. Demand for bracket assemblies (X) is 128 units. The following is the BOM in indented form: DESCRIPTION Bracket assembly Wall board Hanger subassembly Hanger casting Ceramic knob Rivet head screw Metal tong Plastic cap USAGE 1 ITEM X A B D E 5 F G 3 1 Below is a table indicating current inventory levels: Item X 26 D 196 F G 95 Inventory 17 69 17 145 1,220 b. What are the net requirements for each item? (Leave no cells blank - be certain to enter "0" wherever required.) Item Net Requirements A B C D F Garrow_forward13. The Bi-Product Company produces two products (A and B) that are similar in terms of labor con- tent and skills required. Company management wishes to "level" the number of employees needed each day so no hiring or layoffs will be required during the year. A complication to this problem is that the number of working days in each quarter varies. Demand Quarter Product A Product B Working Days 1 9,800 14,500 68 2 12,000 30,000 56 3 14,000 19,500 62 4 31,000 25,000 58 Beginning inventory: 2,400 units of Product A 900 units of Product B Inventory holding cost: $10 per unit per quarter (either product) No back orders allowed No variations in size of workforce allowed Output rate=25 units of either product per day per employee a. What daily production rate will be required to meet the demand forecast and yield zero in- ventory at the end of quarter 4? b. How many employees will be required each day? What are the inventory levels each quarter?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Operations ManagementOperations ManagementISBN:9781259667473Author:William J StevensonPublisher:McGraw-Hill Education
Operations and Supply Chain Management (Mcgraw-hi...Operations ManagementISBN:9781259666100Author:F. Robert Jacobs, Richard B ChasePublisher:McGraw-Hill Education 
Purchasing and Supply Chain ManagementOperations ManagementISBN:9781285869681Author:Robert M. Monczka, Robert B. Handfield, Larry C. Giunipero, James L. PattersonPublisher:Cengage Learning
Production and Operations Analysis, Seventh Editi...Operations ManagementISBN:9781478623069Author:Steven Nahmias, Tava Lennon OlsenPublisher:Waveland Press, Inc.
Practical Management Science
Operations Management
ISBN:9781337406659
Author:WINSTON, Wayne L.
Publisher:Cengage,
Operations Management
Operations Management
ISBN:9781259667473
Author:William J Stevenson
Publisher:McGraw-Hill Education
Operations and Supply Chain Management (Mcgraw-hi...
Operations Management
ISBN:9781259666100
Author:F. Robert Jacobs, Richard B Chase
Publisher:McGraw-Hill Education
Purchasing and Supply Chain Management
Operations Management
ISBN:9781285869681
Author:Robert M. Monczka, Robert B. Handfield, Larry C. Giunipero, James L. Patterson
Publisher:Cengage Learning
Production and Operations Analysis, Seventh Editi...
Operations Management
ISBN:9781478623069
Author:Steven Nahmias, Tava Lennon Olsen
Publisher:Waveland Press, Inc.