
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Topic Video
Question

Transcribed Image Text:A factory manufactures three products, A, B, and C. Each product requires the use of two machines,
Machine I and Machine II. The total hours available, respectively, on Machine I and Machine Il per
month are 8,080 and 8,350. The time requirements and profit per unit for each product are listed
below.
A
Machine I
10
10
Machine II 6
10
12
Profit
$10 $16 $18
How many units of each product should be manufactured to maximize profit, and what Is the
maximum profit?
Start by setting up the linear programming problem, with A, B, and C representing the number of
units of each product that are produced.
Maximize P%3=
subject to:
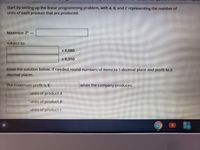
Transcribed Image Text:Start by setting up the linear programming problem, with A, B, and C representing the number of
unlts of each product that are produced.
Maximlze P=
subject to:
< 8,080
< 8,350
Enter the solutlon below. If needed round numbers of items to 1 decimal place and profit to 2
decimal places.
The maximum profit is $
when the company produces:
units of product A
units of product B
units of product C
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 6 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- There are three factories located at AR, IN, and TX respectively. From these locations, a certain commodity is to be delivered to each of the two warehouses situated at A and B. The revenue per commodity item is $10. The weekly demand of the warehouse A and B are respectively 50 and 35 units of the commodity while the production capacity of the factories at AR, IN, and TX are respectively 28, 22, and 35 units. The cost of transportation per unit is given as belows. Cost Warehouse A Warehouse B AR 5 3 IN 6 6 TX 2 4 To maintain a good relationship with all the factories, warehouse B requires that it receives at least 40% of its product from factory in TX. Realize that it is making good profit in warehouse A, AR requires that at least 35% of its product shipped to warehouse A. Formulate (without solving) a linear programming problem to maximize the profit.arrow_forwardFrom the data given compute the sales price for each product T and O. From the data given compute variable cost per unit for each product T and O. Letter Co. produces and sells two products, T and O. It manufactures these products in separate factories and markets them through different channels. They have no shared costs. This year, the company sold 50,000 units of each product. Sales and costs for each product follow.arrow_forwardA small company manufactures three different electronic components for computers. Component A requires 2 hours of fabrication and 1 hour of assembly; component B requires 3 hours of fabrication and 1 hour of assembly; and component C requires 2 hours of fabrication and 2 hours of assembly. The company has up to 900 labor-hours of fabrication time and 700 labor-hours of assembly time available per week. The profit on each component, A, B, and C, is $7, $8, and $10, respectively. How many components of each type should the company manufacture each week in order to maximize its profit (assuming that all components manufactured can be sold)? What is the maximum profit? Let x₁, x2, and x3 be the numbers of components A, B, and C, respectively, that get manufactured. Construct a mathematical model in the form of a linear programming problem. Maximize P=[ subject to X1, X₂, X3 20 The company should manufacture (Simplify your answers.) Fabrication time restriction Assembly time restriction…arrow_forward
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

