
Computer Networking: A Top-Down Approach (7th Edition)
7th Edition
ISBN: 9780133594140
Author: James Kurose, Keith Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
a) Draw the connected subgraph of the given graph above which contains only four nodes ACGB and is also a minimum spanning tree with these four nodes. What is its weighted sum? Draw the adjacency matrix representation of this subgraph (use boolean matrix with only 0 or 1, to show its adjacency in this case).
b) Find the shortest path ONLY from source node D to destination node G of the given graph above, using Dijkstra’s
c) Draw ONLY the shortest path obtained above, and indicate the weight in each edge in the diagram. Also determine the weighted sum
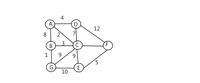
Transcribed Image Text:4
A
D
12
8 2
7
3.
B
C
F
1
9.
9.
G
E
10
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps with 2 images

Knowledge Booster
Similar questions
- Pick the correct statements for the attached directed graph for a toy world wide web. 1. There are exactly six columns having a 1 as an entry. 2. If a new edge from node I to F is added, the resulting graph is strongly connected. 3. The smallest non-zero element in the link matrix is 1/4. 4. The link matrix Q has a column of all zeros. 5. The link matrix is a reducible matrix.arrow_forward7. Consider the following graph: A 14 CO D 9 E C 12 10 17 b) What is the weight of the minimum spanning tree? B Apply Kruskal's algorithm to find the minimum spanning tree. Edges are sorted first by length, and in the event of a tie, by name, where the two letters are in alphabetical order. Use makeset (x), find (x), and union (x, y) to determine if there are cycles. a) Circle the edges that are part of the minimum spanning tree. AC, AD, AE, BC, BD, BE, DE c) Draw the tree that results from applying the union-find algorithm for cycle detection. When drawing the tree, put vertices with lower letters in the left subtrees so that all the vertices in a level are sorted alphabetically from left to rightarrow_forwardQuestion 8. A connected graph G has 4 vertices and 4 edges of costs 1, 2, 3 and respectively 4. (a) Show that G is not a tree. (b) Show that G has a single minimum spanning tree. (Hint: For example, think how Prim's algorithm constructs the minimum spanning tree). (c) Draw a connected graph G with 4 nodes and 4 edges of costs 1, 2, 3, 4, respectively, so that the minimum spanning tree contains the edge of cost 4. The 4 nodes are below, you need to draw the 4 edges and indicate their cost. a O b darrow_forward
- Consider an undirected graph G with 100 nodes. The maximum number of edges to be included in G so that the graph is not connected isarrow_forwardPlease written by computer sourcearrow_forwardGiven the following graph, A C 3 1 E 4 В F 7 D 5 What is the next edge and vertex(s) to be included in the solution if a. we are using Prim's algorithm to find a minimum spanning tree and we have started with vertex E? Edge: Vertex(s): What is the next edge and vertex(s) to be included in the solution if b. we are using Kruskal's algorithm to find a minimum spanning tree Edge: Vertex(s): What is the next edge and vertex(s) to be included in the solution if c. we are using Dijkstra's shortest path algorithm to find shortest paths and we have started with vertex E, with C and F already included in the shortest path tree? Edge: Vertex(s):arrow_forward
- Given N cities represented as vertices V₁, V2,..., UN on an undirected graph (i.e., each edge can be traversed in both directions). The graph is fully-connected where the edge eij connecting any two vertices v; and vj is the straight-line distance between these two cities. We want to search for the shortest path from v₁ (the source) to VN (the destination). Assume that all edges have different values, and e₁, has the largest value among the edges. That is, the source and destination have the largest straight-line distance. Compare the lists of explored vertices when we run the uniform-cost search and the A* search for this problem. Hint: The straight-line distance is the shortest path between any two cities. If you do not know how to start, try to run the algorithms by hand on some small cases first; but remember to make sure your graphs satisfy the conditions in the question.arrow_forwardLet G = (V, E) be an undirected graph and each edge e ∈ E is associated with a positive weight ℓ(e).For simplicity we assume weights are distinct. Is the following statement true or false? Let T be a minimum spanning tree for the graph with the original weight. Suppose we replace eachedge weight ℓ(e) with ℓ(e)^2, then T is still a minimum spanning tree.arrow_forwardYou are given a weighted tree T.(As a reminder, a tree T is a graph that is connected and contains no cycle.) Each node of the tree T has a weight, denoted by w(v). You want to select a subset of tree nodes, such that weight of the selected nodes is maximized, and if a node is selected, then none of its neighbors are selected.arrow_forward
- Write to code describes how to create the links dataset that represents the input graph. In this particular case, the links represent a directed network. The links dataset has only the nodes identification, which means, the from and to variables. The link weights in the transitive closure problem are irrelevant. In other words, it doesn’t matter the cost or the weight of the links, the algorithm searches for the possible paths to connect the nodes within the input graph. If there is a link or a set of links, no matter the weights, that connects node i to node j, that is the matter.arrow_forwardQuestion 1: In graph theory, a graph X is a "complement" of a graph F if which of the following is true? Select one: a. If X is isomorph to F, then X is a complement of F. b. If X has half of the vertices of F (or if F has half of the vertices of X) then X is a complement of F. c. If X has the same vertex set as F, and as its edges ONLY all possible edges NOT contained in F, then X is a complement of F. d. If X is NOT isomorph to F, then X is a complement of F. Question 2: Which statement is NOT true about Merge Sort Algorithm: Select one: a. Merge Sort time complexity for worst case scenarios is: O(n log n) b. Merge Sort is a quadratic sorting algorithm c. Merge Sort key disadvantage is space overhead as compared to Bubble Sort, Selection Sort and Insertion Sort. d. Merge Sort adopts recursive approacharrow_forwardWe recollect that Kruskal's Algorithm is used to fi nd the minimum spanning tree in a weighted graph. Given a weighted undirected graph G = (V , E, W), with n vertices/nodes, the algorithm will fi rst sort the edges in E according to their weights. It will then select (n-1) edges with smallest weights that do not form a cycle. (A cycle in a graph is a path along the edges of a graph that starts at a node and ends at the same node after visiting at least one other node and not traversing any of the edges more than once.) Use Kruskal's Algorithm to nd the weight of the minimum spanning tree for the following graph.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON
Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science
Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning
Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning
Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education
Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY
Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY

Computer Networking: A Top-Down Approach (7th Edi...
Computer Engineering
ISBN:9780133594140
Author:James Kurose, Keith Ross
Publisher:PEARSON

Computer Organization and Design MIPS Edition, Fi...
Computer Engineering
ISBN:9780124077263
Author:David A. Patterson, John L. Hennessy
Publisher:Elsevier Science

Network+ Guide to Networks (MindTap Course List)
Computer Engineering
ISBN:9781337569330
Author:Jill West, Tamara Dean, Jean Andrews
Publisher:Cengage Learning

Concepts of Database Management
Computer Engineering
ISBN:9781337093422
Author:Joy L. Starks, Philip J. Pratt, Mary Z. Last
Publisher:Cengage Learning

Prelude to Programming
Computer Engineering
ISBN:9780133750423
Author:VENIT, Stewart
Publisher:Pearson Education

Sc Business Data Communications and Networking, T...
Computer Engineering
ISBN:9781119368830
Author:FITZGERALD
Publisher:WILEY