
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
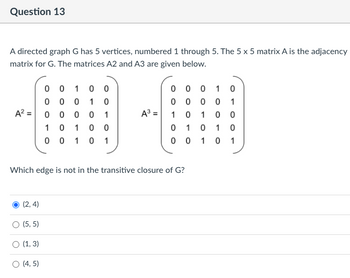
Transcribed Image Text:Question 13
A directed graph G has 5 vertices, numbered 1 through 5. The 5 x 5 matrix A is the adjacency
matrix for G. The matrices A2 and A3 are given below.
00100
0
0
0
1 0
0 0 0 1 0
10
0 0
0
0
1
A20000 1
A³ =
1 0
1
0
0
10 10 0
01
0 1 0
0 0 1 0 1
00101
Which edge is not in the transitive closure of G?
(2,4)
○ (5,5)
○ (1, 3)
○ (4,5)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Similar questions
- Let H be a graph with the following adjacency matrix: 0 1 1 1] 01 1001 [1 1 1 (a) Draw H. Is H a tree? Justify your answer. A = (b) Compute A². What is the meaning of the number in the first row and first column of A²? (c) Could the matrix A² be the adjacency matrix of a simple graph? If so, draw the graph. If not, explain why.arrow_forwardFind, if possible, an invertible matrix P and a diago- nal matrix D such that A = PDP-. Otherwise, explain why A is not diagonalizable. 5 1 2 1 4 1 -3 -2 0 -(t - 3)³arrow_forwardConsider the adjacency matrix 0 0 1 1 1 0 0 0 0 1 0 1 1 0 0 1 1 0 1 1 1 0 1 1 of a graph with nodes labeled a,b,c,d,e and f and lexiographically ordered rows and columns. 1 0 1 1 0 0 Lo 1 0 1 0 0 Suppose the above adjacency matrix identifies the network in a small company, where nodes represent workers and edges indicate that those workers interact during the week. The company has a single team leader and two different projects, one larger than the other. Workers in the same project interact often during the week. b) State whether all workers are involved in at least one project and whether there is any worker, apart from the team leader, who works simultaneously on both projects.arrow_forward
- Help with number 4 please, a and barrow_forwardA square matrix A of size n is idempotent if A2 = A. Show that if A is idempotent, then so is I - A, where I is the identity matrix of size n.arrow_forwardDetermine whether the graphs G1, G2 with the following adjacency matrices are isomorphic: 0 10 00 1 0 1 1 0 0 0 1 0 1 0 0 A1 = A2 0 1 1 0 10 0 0 0 1 0 1 1000 10 = 0 1 0 1 1 0 100101 0 0 0 0 1 1 1 1 0 0 0 0 1 0 1 0 0 0 1000 01arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

