A dam is shaped like a parabola (y = x^2) and has a height of 150 meters. The water's density is 1000kg/m3. Pt 1. FInd the total energy stored by this dam. Pt 2. If fourty-percent of the total energy from the dam was consumed, what would be the water level's new hight? Pt 3. If a city was using this dam for its energy and consumed 12 x 107 MW of power, how much time would it take for the level of the dam to drop down to the height in part 2?
A dam is shaped like a parabola (y = x^2) and has a height of 150 meters. The water's density is 1000kg/m3.
Pt 1. FInd the total energy stored by this dam.
Pt 2. If fourty-percent of the total energy from the dam was consumed, what would be the water level's new hight?
Pt 3. If a city was using this dam for its energy and consumed 12 x 107 MW of power, how much time would it take for the level of the dam to drop down to the height in part 2?
Given:-
The shape of the dam is parabolic with equation y=x2
Height of the dam (H) = 150 m
Density of the water = 1000 kg/m3
To find :-
a) The total energy stored by the dam
b) If 40% of the total energy from the dam was consumed, what would be the water level's new height
c) If city consume 12 x 107 MW of power, how much time would it take for the level of the dam to drop down to the height in b) part.
The two type of energy is stored by the dam when it is full , one is potential energy and the other one is kinetic energy. So, total energy stored will be:
T.E = P.E + K.E
where,
T.E = Total energy
P.E = Potential energy given by formula (m x g x h)
K.E = Kinetic Energy given by the formula (1/2 x m x v2)
T.E= m x g x h+ 1/2 x m x v2
a)
The shape of the dam is parabolic with equation y= x2
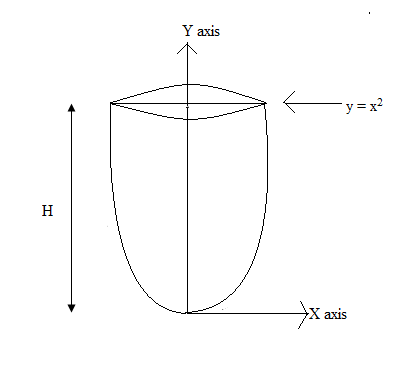
Volume of the parabola with equation y =x2
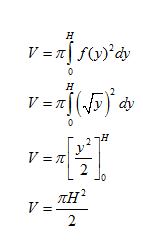
Therefore,
Total energy stored in dam = (mgh)+(1/2mv2)
As the fluid is at rest
so, v=0
therefore,
T.E= (mgh)
we know that ,
Density = mass/volume
or mass = density × volume
So, on putting value of mass in total energy equation
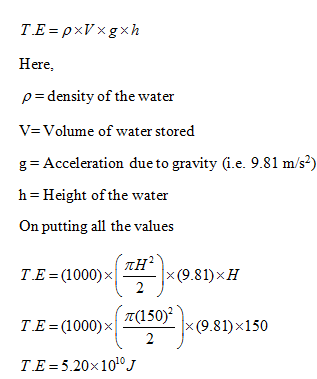
Therefore, total energy stored in parabolic dam is 5.20 x 1010 J
Step by step
Solved in 5 steps with 4 images









