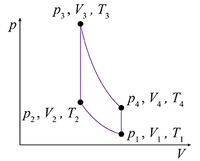
Problem 6: A certain gasoline engine is modeled as a monatomic ideal gas undergoing an Otto cycle, represented by the p-V diagram shown in the figure. The initial pressure, volume, and temperature are p1 = 0.95 × 105 Pa, V1 = 0.025 m3, and T1 = 310 K, respectively.
Part (a) Calculate the number of moles times the gas constant, nR, in joules per kelvin, to three significant figures, using the ideal-
Part (b) Calculate the work performed on the gas during the first step, in joules, for V2 = V1/6.2.
Part (c) Calculate the temperature of the gas, in kelvins, at the end of the first step.
Part (d) The second step in the Otto cycle is isochoric (constant-volume) heating. Calculate the heat absorbed by the gas during this process, in joules, if the temperature is increased so that T3 = 1.53T2.
Part (e) Calculate the pressure at the end of the isochoric heating step, in pascals, to three significant figures.
Part (f) The third step in the Otto cycle is adiabatic expansion, which brings the volume back to its initial value. Calculate the work preformed on the gas, in joules, during the third step.
Part (g) The fourth and last step in the Otto cycle is isochoric cooling to the initial conditions. Find the amount of heat, in joules, that is discharged by the gas during the fourth step.
Part (h) Calculate the efficiency of this Otto cycle, expressed as a percent.
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 3 images

- Suppose you have 0.53 moles of an ideal gas. What is the average kinetic energy of that gas (in units of kJ) if the temperature of the gas is 280.2K? Note: It is understood that the unit of your answer is some number of kilo-Joules, however do not explicitly include units in your answer. Enter only a number. If you do enter a unit ("kJ" in this case), you answer will be counted wrong.arrow_forwardHelp pleasearrow_forwardREAL GASES n=1 mol of real gas is in a container with a volume of v=0.25lt. The pressure of the gas at T1=300K temperature is p1=90atm, and at T2=350K the pressure of the gas is P2=110atm. Find the Vanderwaals constants (a and b) for this gas.arrow_forward
- The heat engine shown in the figure uses 2.0 mol of a monatomic gas as the working substance. (Figure 1) Figure p (kPa) 600 400 200 0 0 0.025 0.050 < 1 of 1 V (m³) Part D Determine AEth, Ws, and Q for 3→1. Enter your answers numerically separated by commas. Express your answer using two significant figures. VE ΑΣΦ AEth, Ws, Q = Submit Part E Request Answer What is the engine's thermal efficiency? Express your answer using two significant figures. ? Jarrow_forward4.5 mol of monatomic gas A interacts with 2.9 mol of monatomic gas B. Gas A initially has 9000 J of thermal energy, but in the process of coming to thermal equilibrium it transfers 800 J of heat energy to gas B. How much thermal energy did gas B have initially? Express your answer with the appropriate units. ► View Available Hint(s) EBi = Submit Value 4 Previous Answers Units ?arrow_forwardA balloon is filled with helium gas at atmospheric pressure (1 atm) until its volume is 800 m³. The helium gas is then transferred to cylinders that have a volume of 2.3 m³ at a pres- sure of 13.3 atm. Calculate the number of cylinders used. Assume that the temperature of the helium gas remains constant. (1 atm = 1.013 × 105 Pa).arrow_forward
- When gas expands in a cylinder with radius r, the pressure P at any given time is a function of the volume V: P = P(V). The force exerted by the gas on the piston (see the figure) is the product of the pressure and the area: F = πr²p. piston head V x The work done by the gas when the volume expands from volume V₁ to volume V2 is as follows. 1 W = dv In a steam engine the pressure and volume of steam satisfy the equation PV1.4 = k, where k is a constant. (This is true for adiabatic expansion, that is, expansion in which there is no heat transfer between the cylinder and its surroundings.) Calculate the work done by the engine during a cycle when the steam starts at a pressure of 180 lb/in² and a volume of 500 in³ and expands to a volume of 700 in³. (Round your answer to two decimal places.) W = X ft-lbarrow_forwardThe heat engine shown in the figure uses 2.0 mol of a monatomic gas as the working substance. (Figure 1) Figure p (kPa) 600 400 200 0 0 0.025 0.050 V (m³) 1 of 1 Part A Determine T₁, T2, and T3. Enter your answers numerically separated by commas. Express your answer using two significant figures. T₁, T2, T3 = 600,1800,1200 K Submit Previous Answers Correct Part Barrow_forwardThe pressure P (in kilopascals), volume V (in liters), and temperature T (in kelvins) of a mole of an ideal gas are related by the equation PV = 8.317. Find the rate at which the volume is changing when the temperature is 325 K and increasing at a rate of 0.05 K/s and the pressure is 29 and increasing at a rate of 0.07 kPa/s. Please show your answers to at least 4 decimal places. dV dt L/sarrow_forward
- Problem 3. The viral coefficients of a gas at 20 °C and 11.5 bar are B = -138 cm³ mol¹ and C=7222 cmº mol². Calculate the V (molar volume) Z (compressibility factor) of the gas. Use the equation below (R = 83.14 cm³ bar mol-¹ K-¹). PV 2 = ² = (1 + = + =) Z RTarrow_forwardA given gas is heated from 273 K to 546K, while its volume is doubled. If initially the gas pressure is 4 x 105 Pascal, the final pressure is: A-P = 4 × 105 Pascal B- P = 2 x 105 Pascal C- P = 1 × 105 Pascal D- P = 0.5 x 105 Pascal E- P = 0.25 x 105 Pascal O A Ос D ОЕarrow_forward