
Concept explainers
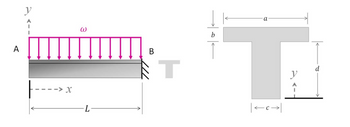
A cantilever beam with a ‘T’ shaped cross-section is loaded with a distributed load as shown below.
The intensity of the distributed load is 100N/mm. b = 6.25mm and c=6.25mm.
Parameter Description Value Units
L - Beam length 250 mm
a - Width of the flange 80 mm
d - Height of the web 75 mm
σ - Yield stress 250 MPa
You are tasked with ensuring the beam can withstand the applied loading. To do this you must:
a) Calculate the centroid for the given cross-section. Your value of ?ത should be measured from
the bottom of the section. Determine an expression for Q (statical moment of area) for the
given shape. The expression(s) for Q should be in terms of the variable, y, measured from the
bottom of the section.
b) Create a graph of the shear and bending stresses at the fixed support (B) over the crosssection. The stresses should be plotted as a function of y, measured from the bottom of the
section.
Trending nowThis is a popular solution!
Step by stepSolved in 6 steps with 10 images

- I5KN Draw and label the V and M diagrams. Fill in the blanks. Find M- max and the equations for q, V, and M in the region 3arrow_forwardaf 11. Iff= show that y √(1-2xy + y²) (x-y) ax afarrow_forwardH.W: find and ди 8/8 Əz as functions of u and v if: z=4en y, x = ln(ucosv), y=usin varrow_forward12. If z = x.f)+F). prove that az (i) x ax a² z +2xy ax. ay a2z +y2. =0 ay 2arrow_forward(8.) Draw the following network: a. G follows F but precede H b. G follows D but precede J c. M follows H but precede L d. K follows A but precede L e. F follows A f. A and D start at the same time g. J and L terminate at the same time.arrow_forwardFind Ix for the shape below: 2.0 2.0 Ix: Componen Ai 1.0 |ΣΑΙ = Yave = [Aiyi/[Ai = dy = Yave - yi = |lx = Elxi + [A(dy2) = 3.0 8.0 yi Aiyi = Aiyi [lxi = Ixi dy ZA(dy)= Ai(dy)arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios

 Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON
Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
 Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning





