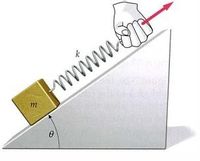
A block of mass m rests on a plane inclined at θ with the horizontal. The block is attached to a spring of constant k as shown in Figure-2. The coefficients of static and kinetic friction between the block and plane are and respectively. Very slowly, the spring is pulled upward along the plane until the block starts to move.   (a) Obtain an expression for the extension d of the spring the instant the block moves. (b) Determine the value of such that the block comes to rest just as the spring is in its unstressed condition, that is, neither extended nor compressed.

Learning Goal: To understand the Equipartition Theorem and its implications for the mechanical motion of small objects. In statistical mechanics, thermal energy is the random motion of the microscopic world. The average kinetic or potential energy of each degree of freedom of the microscopic world therefore depends on the temperature. If heat is added, molecules increase their translational and rotational speeds, and the atoms constituting the molecules vibrate with larger amplitude about their equilibrium positions. It is a fact of nature that the energy of each degree of freedom is determined solely by the temperature. The Equipartition Theorem states this quantitatively: The average energy associated with each degree of freedom in a system at absolute temperature T is (1/2)k³T, where KB = : 1.38 × 10-2³ J/K is Boltzmann's constant. A "degree of freedom" corresponds to any dynamical variable that appears quadratically in the energy. For instance, (1/2)mv² is the kinetic energy of a…

A 15 kg block sliding horizontally across the floor has a coefficient of static friction of μs = 0.49 and a coefficient of kinetic friction of μk = 0.34. If it was sliding at an initial speed of 4.2 m/s, how far will it travel before stopping? Be clear and show all your work. (Dynamics)

please answer all with steps

Using the geometrical approach based on areas just described in question 1, you can find the total work done by the approximate force over the displacement between x = 0 and x = x2. What is this approximate work for the case of N = 4?

A box with weight of magnitude FG=2.00N is lowered by a rope down a smooth plane that is inclined at an angle ϕ = 30.0 ∘ above the horizontal, as shown in (Figure 1) at left. The normal force acting on the box has a magnitude n=1.73N the tension force is 1.00 N, and the displacement Δr of the box is 1.80 m down the inclined plane. The work done on the box by gravity is 1.8 J What is the work Wn done on the box by the normal force? What is the work WT done by the tension force?

Only parts A & B please.