Question
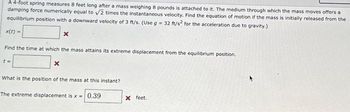
Transcribed Image Text:A 4-foot spring measures 8 feet long after a mass weighing 8 pounds is attached to it. The medium through which the mass moves offers a
damping force numerically equal to √2 times the instantaneous velocity. Find the equation of motion if the mass is initially released from the
equilibrium position with a downward velocity of 3 ft/s. (Use g = 32 ft/s² for the acceleration due to gravity.)
x(t) =
Find the time at which the mass attains its extreme displacement from the equilibrium position.
t=
X
x
What is the position of the mass at this instant?
The extreme displacement is x = 0.39
X feet.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Similar questions
- The oscillatory movement of a simple pendulum is a characteristic of the regular repetition of displacements around an equilibrium position. The pendulum swings due to the restored force of gravity, which seeks to bring the mass back to the equilibrium point. The oscillatory behavior is described by a trigonometric solution, which relates the pendulum's position to time, considering its amplitude, frequency and initial phase. Statement: A simple pendulum moves according to the following question:y(t) = A.sin(ωt + φ)In this question, y(t) is the horizontal position of the pendulum, A is its amplitude, ω is its angular velocity, given by ω = 2πf, and φ is the initial phase of the movement, in radians. Since the initial phase of the movement is equal to 0 and its angular velocity is π/2 rad/s, the oscillation frequency of this pendulum is correctly given by the alternative: a) 2.0Hz b) 1.5Hz c) 1.0Hz d) 0.5Hz e) 0.25Hzarrow_forwardA force of 9 pounds stretches a spring 1 foot. A mass weighing 6.4 pounds is attached to the spring, and the system is then immersed in a medium that offers a damping force numerically equal to 1.2 times the instantaneous velocity. (a) Find the equation of motion if the mass is initially released from rest from a point 1 foot above the equilibrium position. ft x(t) = = -λt (b) Express the equation of motion in the form x(t) = Ae¯ sin(√²-2²t+ x(t) = = ft q²t + 9), which is given in (23) of Section 3.8. (Round p to two decimal places.) (c) Find the first time at which the mass passes through the equilibrium position heading upward. (Round your answer to three decimal places.) Sarrow_forwardIn order to study the long-term effects of weightlessness, astronauts in space must be weighed (or at least "massed"). One way in which this is done is to seat them in a chair of known mass attached to a spring of known force constant and measure the period of the oscillations of this system. The 35.6 kg chair alone oscillates with a period of 1.30 s, and the period with the astronaut sitting in the chair is 2.23 s Part A Find the force constant of the spring. k= Submit Request Answer Part B VE ΑΣΦ Find the mass of the astronaut. m = [-] ΑΣΦ 1 Submit Request Answer ? N/m kgarrow_forward
- A block of mass m = 1 is sitting on a table and is attached to a spring of strength k = 5 so that it can slide horizontally on the table. The coefficient of linear friction between the block and the table is b = 2, and an external force of F(t) = 13 cos(3t) acts on it. Find the general solution to this differential equation, and determine if the spring--mass system is over-damped, critically damped, or under-damped.arrow_forwardShow that the function x(t) = A cos ω1t oscillates with a frequency ν = ω1/2π. What is the frequency of oscillation of the square of this function, y(t) = [A cos ω1t]2? Show that y(t) can also be written as y(t) = B cos ω2t + C and find the constants B, C, and ω2 in terms of A and ω1arrow_forwardA box of mass 0.850 kg is attached to a spring with k = 145 N/m and set into simple harmonic motion on a frictionless, horizontal table. The amplitude of motion is 5.10 cm. (Use the exact values you enter in previous answer(s) to make later calculation(s).) (a) What is the total energy of the box–spring system? ______ J (b) What is the speed of the box when the spring is compressed by 2.00 cm? (Give your answer to at least two decimal places.) ______m/s (c) What is the kinetic energy of the box at this position? ______ J (d) What is the potential energy of the box–spring system at this position? ______ Jarrow_forward
- A mass weighting 24 lbs stretches a spring 4 inches. The mass is in a medium that exerts a damping force of 57 lbs when the mass has a speed of 6 ft/sec. Suppose the object is displaced an additional 8 inches and released. Find an equation for the object's displacement, u(t), in feet after t seconds. u(t) = Use the convention: If the displacement is upward then u <0arrow_forwardIn order to study the long-term effects of weightlessness, astronauts in space must be weighed (or at least "massed"). One way in which this is done is to seat them in a chair of known mass attached to a spring of known force constant and measure the period of the oscillations of this system. The 34.6-kg chair alone oscillates with a period of 1.45 s, and the period with the astronaut sitting in the chair is 2.21 s. (A) Find the force constant of the spring. Express your answer in newtons per meter. (B) Find the mass of the astronaut. Express your answer in kilograms.arrow_forwardA 3 kilogram weight stretches a spring by 8 cm. The mass-spring system is immersed in a damping fluid which exerts a force of 0.5 N when the mass is traveling 0.25 m/sec. Write a differential equation for u(t), the displacement of the mass at time t. (use g = 9.8 m/sec ^2 .)arrow_forward
- Let there be a mass M = 0.5 kg on a spring. a) If we can hang the mass on the spring in a vertical position, how can we measure the spring constant, k, of the spring? Now we use this same spring in the horizontal configuration, assuming the mass slides on a frictionless horizontal surface. b) Assuming we have measured k to be 10 N/m, how many times will the system oscillate in a minute? (assume we displace the mass from equilibrium so that the system oscillates) c) If the mass passes through the equilibrium position with a velocity vo at time t = 0, what is the amplitude of the oscillation? d) Write the equation for the horizontal displacement of the block as a function of time.arrow_forwardThe equation of motion for a damped harmonic oscillator is s(t) = Ae^(−kt) sin(ωt + δ),where A, k, ω, δ are constants. (This represents, for example, the position of springrelative to its rest position if it is restricted from freely oscillating as it normally would).(a) Find the velocity of the oscillator at any time t.(b) At what time(s) is the oscillator stopped?arrow_forwardThe graph shown in the figure (Figure 1) closely approximates the displacement at of a tuning fork as a function of time t as it is playing a single note. Figure x(mm) 0.4 0.2 -0.2 -0.4 AMA 2 (ms) 1 of 1 What is the amplitude of this fork's motion? A = Submit Part B T = What is the period of this fork's motion? Submit Part C | ΑΣΦ Request Answer | ΑΣΦ What is the frequency of this fork's motion? f = 426 Part D Request Answer ΠΑΣΦ Submit Previous Answers Request Answer w = 2π (224) What is the angular frequency of this fork's motion? ID ΑΣΦ ? * Incorrect; Try Again; 4 attempts remaining ? ? ? mm mns Hz rad/s Pearsonarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios