Question
Question 8 please
Thank you
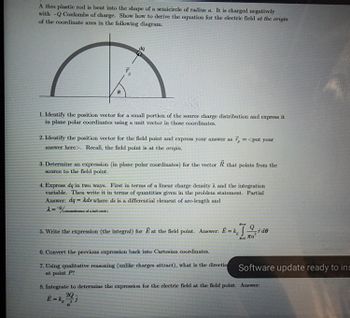
Transcribed Image Text:A thin plastic rod is bent into the shape of a semicircle of radius a. It is charged negatively
with -Q Coulombs of charge. Show how to derive the equation for the electric field at the origin
of the coordinate axes in the following diagram.
8
dq
1. Identify the position vector for a small portion of the source charge distribution and express it
in plane polar coordinates using a unit vector in those coordinates.
2. Identify the position vector for the field point and express your answer as 7 = <put your
answer here>. Recall, the field point is at the origin.
3. Determine an expression (in plane polar coordinates) for the vector R that points from the
source to the field point.
(circunference of a half cicle)
4. Express dq in two ways. First in terms of a linear charge density λ and the integration
variable. Then write it in terms of quantities given in the problem statement. Partial
Answer: dq = Ads where ds is a differential element of arc-length and
2=%ci
8-x
5. Write the expression (the integral) for E at the field point. Answer: E = kde
Ла
6. Convert the previous expression back into Cartesian coordinates.
7. Using qualitative reasoning (unlike charges attract), what is the directio
at point P?
Software update ready to ins
8. Integrate to determine the expression for the electric field at the field point. Answer:
E =k, 20
-j
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
arrow_back_ios
arrow_forward_ios