7.43 *** (Computer] Consider a massless wheel of radius R mounted on a frictionless horizontal axis. A point máss M is glued to the edge, and a massless string is wrapped several times around the perimeter and hangs vertically down with a mass m suspended from its bottom end. (See Figure 4.28.) Initially I am holding the wheel with M vertically below the axle. At 1 = 0, I release the wheel, and m starts to fall vertically down. (a) Write down the Lagrangian L = T - U as a function of the angle o through which the wheel has turned. Find the equation of motion and show that, provided m < M, there is one position of stable equilibrium. (b) Assuming m < M, sketch the potential energy U () for -n < ¢ < 47 and use your graph to explain the equilibrium position you found. (c) Because the equation of motion cannot be solved in terms of elementary functions, you are going to solve it numerically. This requires that you choose numerical values for the various parameters. Take M = g = R = 1 (this amounts to a convenient choice of units) and m = 0.7. Before solving the equation make a careful plot of U ($) against o and predict the kind of motion expected when M is released from rest at ø = 0. Now solve the equation of motion for 0 < t < 20 and verify your prediction. (d) Repeat part (c), but with m = 0.8.
7.43 *** (Computer] Consider a massless wheel of radius R mounted on a frictionless horizontal axis. A point máss M is glued to the edge, and a massless string is wrapped several times around the perimeter and hangs vertically down with a mass m suspended from its bottom end. (See Figure 4.28.) Initially I am holding the wheel with M vertically below the axle. At 1 = 0, I release the wheel, and m starts to fall vertically down. (a) Write down the Lagrangian L = T - U as a function of the angle o through which the wheel has turned. Find the equation of motion and show that, provided m < M, there is one position of stable equilibrium. (b) Assuming m < M, sketch the potential energy U () for -n < ¢ < 47 and use your graph to explain the equilibrium position you found. (c) Because the equation of motion cannot be solved in terms of elementary functions, you are going to solve it numerically. This requires that you choose numerical values for the various parameters. Take M = g = R = 1 (this amounts to a convenient choice of units) and m = 0.7. Before solving the equation make a careful plot of U ($) against o and predict the kind of motion expected when M is released from rest at ø = 0. Now solve the equation of motion for 0 < t < 20 and verify your prediction. (d) Repeat part (c), but with m = 0.8.
Elements Of Electromagnetics
7th Edition
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Sadiku, Matthew N. O.
ChapterMA: Math Assessment
Section: Chapter Questions
Problem 1.1MA
Related questions
Question
Classical
Subparts (a), (b) and (c) are required.
Transcribed Image Text:R
M
Figure 4.28
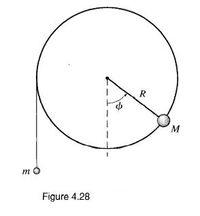
![7.43 *** [Computer] Consider a massless wheel of radius R mounted on a frictionless horizontal axis.
A point máss M is glued to the edge, and a massless string is wrapped several times around the perimeter
and hangs vertically down with a mass m suspended from its bottom end. (See Figure 4.28.) Initially I
am holding the wheel with M vertically below the axle. Ati = 0, I release the wheel, and m starts to fall
vertically down. (a) Write down the Lagrangian L = T - U as a function of the angle ø through which
the wheel has turned. Find the equation of motion and show that, provided m < M, there is one position
of stable equilibrium. (b) Assuming m < M, sketch the potential energy U (4) for --n <¢ < 4n and
use your graph to explain the equilibrium position you found. (c) Because the equation of motion
cannot be solved in terms of elementary functions, you are going to solve it numerically. This requires
that you choose numerical values for the various parameters. Take M = g = R = 1 (this amounts to
a convenient choice of units) and m = 0.7. Before solving the equation make a careful plot of U ($)
against o and predict the kind of motion expected when M is released from rest at ø = 0. Now solve
the equation of motion for 0 <t < 20 and verify your prediction. (d) Repeat part (c), but with m = 0.8.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fc95e35aa-092e-4366-b40b-c3654c0db2c4%2Fc73c1f22-bc4c-4ad7-9ebc-d2af27151104%2Fklzowos_processed.png&w=3840&q=75)
Transcribed Image Text:7.43 *** [Computer] Consider a massless wheel of radius R mounted on a frictionless horizontal axis.
A point máss M is glued to the edge, and a massless string is wrapped several times around the perimeter
and hangs vertically down with a mass m suspended from its bottom end. (See Figure 4.28.) Initially I
am holding the wheel with M vertically below the axle. Ati = 0, I release the wheel, and m starts to fall
vertically down. (a) Write down the Lagrangian L = T - U as a function of the angle ø through which
the wheel has turned. Find the equation of motion and show that, provided m < M, there is one position
of stable equilibrium. (b) Assuming m < M, sketch the potential energy U (4) for --n <¢ < 4n and
use your graph to explain the equilibrium position you found. (c) Because the equation of motion
cannot be solved in terms of elementary functions, you are going to solve it numerically. This requires
that you choose numerical values for the various parameters. Take M = g = R = 1 (this amounts to
a convenient choice of units) and m = 0.7. Before solving the equation make a careful plot of U ($)
against o and predict the kind of motion expected when M is released from rest at ø = 0. Now solve
the equation of motion for 0 <t < 20 and verify your prediction. (d) Repeat part (c), but with m = 0.8.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images
Recommended textbooks for you
Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education
Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:
9781118170519
Author:
Norman S. Nise
Publisher:
WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:
9781337093347
Author:
Barry J. Goodno, James M. Gere
Publisher:
Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:
9781118807330
Author:
James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:
WILEY