Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
37

37

Elementary Geometry For College Students, 7e
Elementary Geometry For College Students, 7e
7th Edition
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.
ChapterP: Preliminary Concepts
SectionP.2: Statements And Reasoning
Problem 2E: In Exercises 1 and 2, which sentences are statements? If a sentence is a statement, classify it as...
See similar textbooks
icon
Related questions
Question

37

 

stify the ent. is w to vilW Each statement in Exercises 33-38 is either true (in all cases) or false (for at least one example). If false, construct a specific example to show that the statement is not always true. Such an hear no example is called a counterexample to the statement. If a statement is true, give a justification. (One specific example cannot explain why a statement is always true. You will have to do more work here than in Exercises 21 and 22.) lie the in ins 32. Given A the - 9 -3 3 plus twice the second column equals the third column. Find a nontrivial solution of Ax = 0. 118d woda 33. If v₁,..., v4 are in R4 and v3 = 2v₁ + V2, then {V1, V2, V3, V4} is linearly dependent. 34. If V₁,..., V4 are in R4 and v3 = 0, then {V₁, V2, V3, V4) is linearly dependent. 35. If v₁ and v₂2 are in R4 and v₂ is not a scalar multiple of V₁, then {V₁, V₂} is linearly independent. 36. If V₁,..., V4 are in R4 and v3 is not a linear combination of V1, V2, V4, then {V1, V2, V3, V4} is linearly independent. 37. If V₁,..., V4 are in R4 and {V1, V2, V3} is linearly dependent, then {V1, V2, V3, V4} is also linearly dependent. 38. If V₁,..., V4 are linearly independent vectors in R4, then {V1, V2, V3} is also linearly independent. [Hint: Think about X₁V₁ + X₂V₂ + X3V3 + 0 V4 = 0.]
Transcribed Image Text:stify the ent. is w to vilW Each statement in Exercises 33-38 is either true (in all cases) or false (for at least one example). If false, construct a specific example to show that the statement is not always true. Such an hear no example is called a counterexample to the statement. If a statement is true, give a justification. (One specific example cannot explain why a statement is always true. You will have to do more work here than in Exercises 21 and 22.) lie the in ins 32. Given A the - 9 -3 3 plus twice the second column equals the third column. Find a nontrivial solution of Ax = 0. 118d woda 33. If v₁,..., v4 are in R4 and v3 = 2v₁ + V2, then {V1, V2, V3, V4} is linearly dependent. 34. If V₁,..., V4 are in R4 and v3 = 0, then {V₁, V2, V3, V4) is linearly dependent. 35. If v₁ and v₂2 are in R4 and v₂ is not a scalar multiple of V₁, then {V₁, V₂} is linearly independent. 36. If V₁,..., V4 are in R4 and v3 is not a linear combination of V1, V2, V4, then {V1, V2, V3, V4} is linearly independent. 37. If V₁,..., V4 are in R4 and {V1, V2, V3} is linearly dependent, then {V1, V2, V3, V4} is also linearly dependent. 38. If V₁,..., V4 are linearly independent vectors in R4, then {V1, V2, V3} is also linearly independent. [Hint: Think about X₁V₁ + X₂V₂ + X3V3 + 0 V4 = 0.]
Expert Solution
Step 1

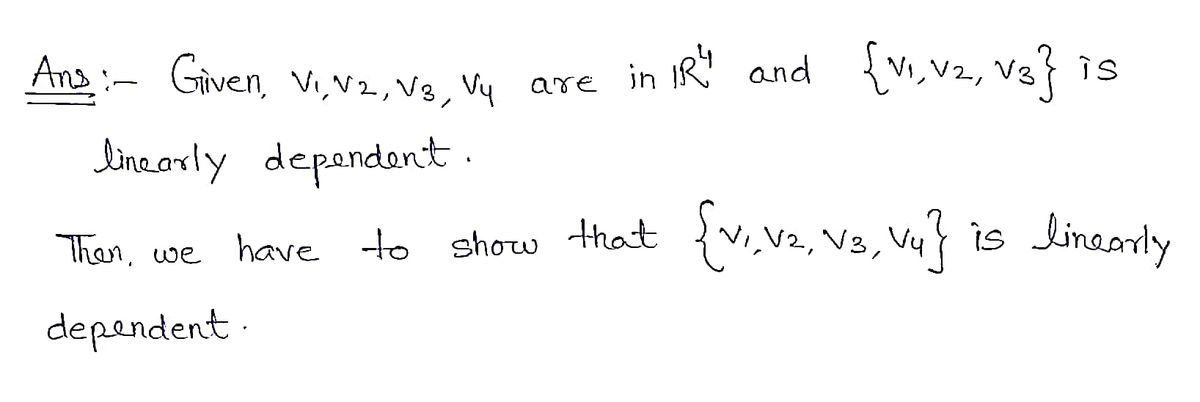
Advanced Math homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer