
Database System Concepts
7th Edition
ISBN: 9780078022159
Author: Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Concept explainers
Question

Transcribed Image Text:**Context-Free Grammars for Specific Languages**
### Example 1:
Language: \{a<sup>n</sup>b<sup>m</sup> : m ≥ n, m-n is even\}
**Context-free grammar for the language:**
```
S -> aSb
S -> Sbb
S -> ε
```
### Example 2:
Language: \{a<sup>i</sup>b<sup>j</sup> : i, j ≥ 0 and 2i = 3j + 1\}
**Context-free grammar for the language:**
```
S -> aaaSbb
S -> aab
```
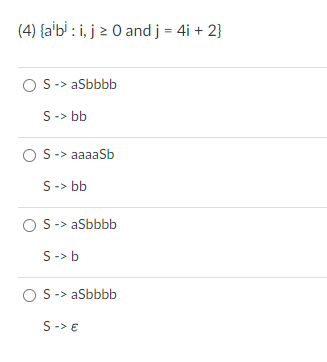
Transcribed Image Text:The image contains a question related to formal languages, specifically about generating strings with a given pattern. It presents a multiple-choice question and several grammar production rules for each option. Here is the detailed transcription:
---
**Question:**
(4) \(\{ a^i b^j : i, j \geq 0 \text{ and } j = 4i + 2 \}\)
What grammar generates the language described by the condition \(j = 4i + 2\)?
**Options:**
1.
- \( S \to aSbbbb \)
- \( S \to bb \)
2.
- \( S \to aaaaSb \)
- \( S \to bb \)
3.
- \( S \to aSbbbb \)
- \( S \to b \)
4.
- \( S \to aSbbbb \)
- \( S \to \varepsilon \)
---
**Explanation:**
This question requires identifying the correct set of production rules that generate strings of the form \( a^i b^j \) where \( j = 4i + 2 \).
- Each option lists productions for the non-terminal \( S \).
- The goal is to derive a pattern where the number of \( b \)'s is exactly four times the number of \( a \)'s plus two.
The correct answer should ensure that starting from \( S \), any string produced should conform to the given relationship between \( i \) and \( j \).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- High Performance Computing Questions/CUDA Programming Given a __global__ function add and a positive integer N, what does the call below mean? add<<< N, 1 >>>(); Given a __device__ function add and a positive integer N, what does the call below mean? add<<< 1, N >>>();arrow_forward#9arrow_forwardAlert: Don't submit AI generated answer and please submit a step by step solution and detail explanation for each steps.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education

Database System Concepts
Computer Science
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:McGraw-Hill Education

Starting Out with Python (4th Edition)
Computer Science
ISBN:9780134444321
Author:Tony Gaddis
Publisher:PEARSON

Digital Fundamentals (11th Edition)
Computer Science
ISBN:9780132737968
Author:Thomas L. Floyd
Publisher:PEARSON

C How to Program (8th Edition)
Computer Science
ISBN:9780133976892
Author:Paul J. Deitel, Harvey Deitel
Publisher:PEARSON

Database Systems: Design, Implementation, & Manag...
Computer Science
ISBN:9781337627900
Author:Carlos Coronel, Steven Morris
Publisher:Cengage Learning

Programmable Logic Controllers
Computer Science
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education