
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
![3. Assume that f : R → R is such that |f(x) – f (y)| < A|x – y| for all x, y E R
and some A E (0,1). Pick xo E R arbitrarily, and construct a sequence (xn)
as follows: n+1
f (xn) for n > 0.
(a) Prove that |Xn+1 – Xn[ < A|xn
Xn-1| for all n > 1.
(b) Prove that |xn+1 – Xn| < \"|x1 – xo] for all n > 1.
(c) Prove that (xn) is convergent.
(d) Let x*
lim xn. Prove that f(x*) = x*.](https://content.bartleby.com/qna-images/question/7fd47556-f3ce-4f39-818d-be563d9523c8/7d48a182-9626-43ba-9f05-bc79cf8ee5aa/y5f7pnl_thumbnail.jpeg)
Transcribed Image Text:3. Assume that f : R → R is such that |f(x) – f (y)| < A|x – y| for all x, y E R
and some A E (0,1). Pick xo E R arbitrarily, and construct a sequence (xn)
as follows: n+1
f (xn) for n > 0.
(a) Prove that |Xn+1 – Xn[ < A|xn
Xn-1| for all n > 1.
(b) Prove that |xn+1 – Xn| < \"|x1 – xo] for all n > 1.
(c) Prove that (xn) is convergent.
(d) Let x*
lim xn. Prove that f(x*) = x*.
Expert Solution
arrow_forward
Step 1
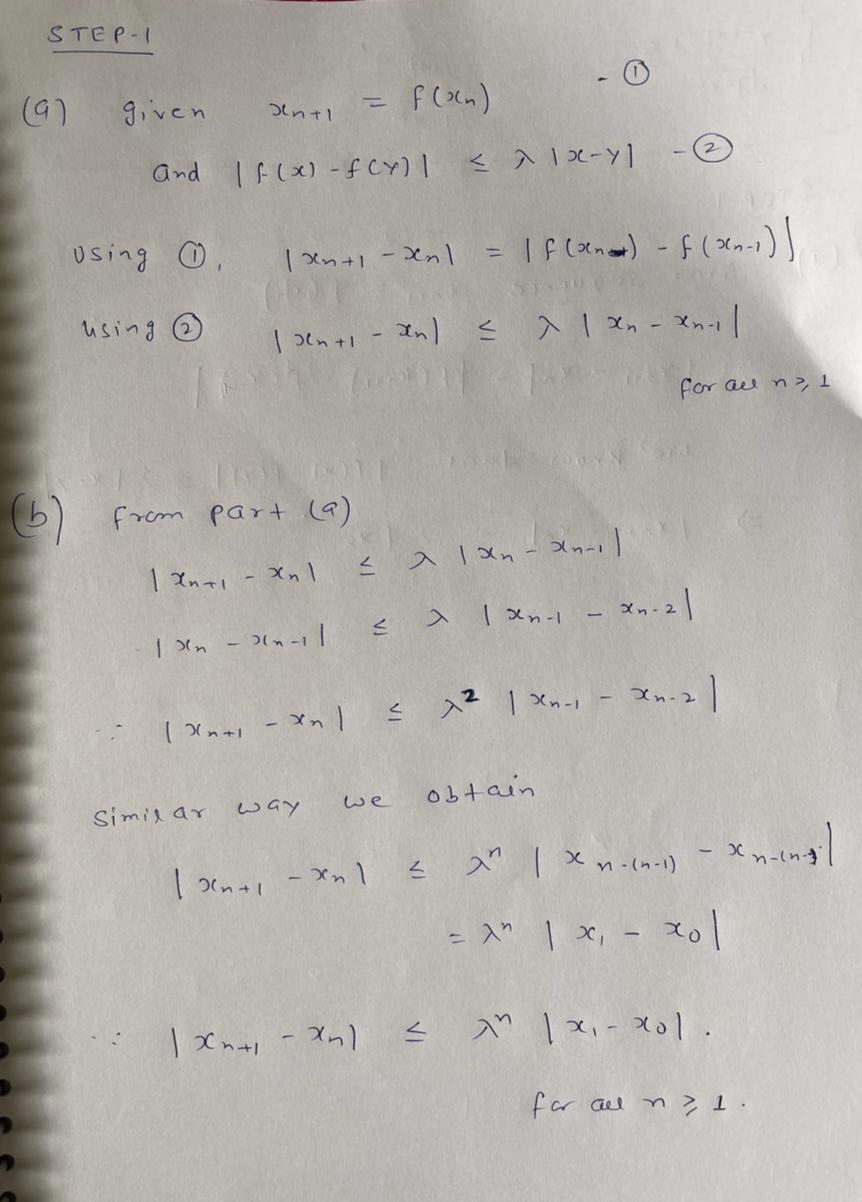
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Let f be a real-valued function with domain R defined by f(x) = x2. Define a sequence (s1, s2, s3, ...) by s1 = b and sj = f(sj-1), for j = 1,2,3,4... a) assume that b=1, and find a formula for sn. b) assume that b=3, and find a formula for sn. c) prove the conjecture in part (b).arrow_forwardConsider the function f : R → R, and define the sequence {an} such that an = f(n). True or False? If lim n→∞ an = L, then lim x→∞ f(x) = L If true prove it, if false,provide a counterexample (i.e. a specific function for which the statement does not hold).arrow_forwardConsider the function f : R → R, and define the sequence {an} such that an = f(n). True or False? If limn→∞ an = l, then limx→∞ f(x) = l. If true prove it, if false, provide a counterexample (i.e. a specific function for which the statement does not hold).arrow_forward
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

