Define a sequence of real numbers (xn) as follows: Let x₁ = 2, and supposing that an has been defined, define 1 2 3+1 = 2 ( x x + ²) Xn+1 . (a) Prove that x2 is always greater than or equal to 2, and then use this to prove that xnxn+1 ≥ 0. [So (n) is decreasing.] Conclude that lim = √2. in (b) For any real number c> 0, define a sequence (yn) so that (yn) converges to √c.
Define a sequence of real numbers (xn) as follows: Let x₁ = 2, and supposing that an has been defined, define 1 2 3+1 = 2 ( x x + ²) Xn+1 . (a) Prove that x2 is always greater than or equal to 2, and then use this to prove that xnxn+1 ≥ 0. [So (n) is decreasing.] Conclude that lim = √2. in (b) For any real number c> 0, define a sequence (yn) so that (yn) converges to √c.
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter4: Polynomial And Rational Functions
Section4.2: Properties Of Division
Problem 51E
Related questions
Question
![follows: Let x₁
Define a sequence of real numbers (n) as
2, and supposing that an has been defined, define
=
to prove that In
lim = √2.
= 1/2 (² ₂ + 2²/1).
Xn
Xn
(a) Prove that x2 is always greater than or equal to 2, and then use this
n+10. [So (n) is decreasing.] Conclude that
-
Xn+1 =
(b) For any real number c > 0, define a sequence (yn) so that (yn)
converges to √c.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ffa923b6f-81dd-482c-8885-6de6bc295751%2F0eaf1ae8-3161-4c6f-9cb5-c9368c8c3416%2Fhiqpcd9_processed.jpeg&w=3840&q=75)
Transcribed Image Text:follows: Let x₁
Define a sequence of real numbers (n) as
2, and supposing that an has been defined, define
=
to prove that In
lim = √2.
= 1/2 (² ₂ + 2²/1).
Xn
Xn
(a) Prove that x2 is always greater than or equal to 2, and then use this
n+10. [So (n) is decreasing.] Conclude that
-
Xn+1 =
(b) For any real number c > 0, define a sequence (yn) so that (yn)
converges to √c.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
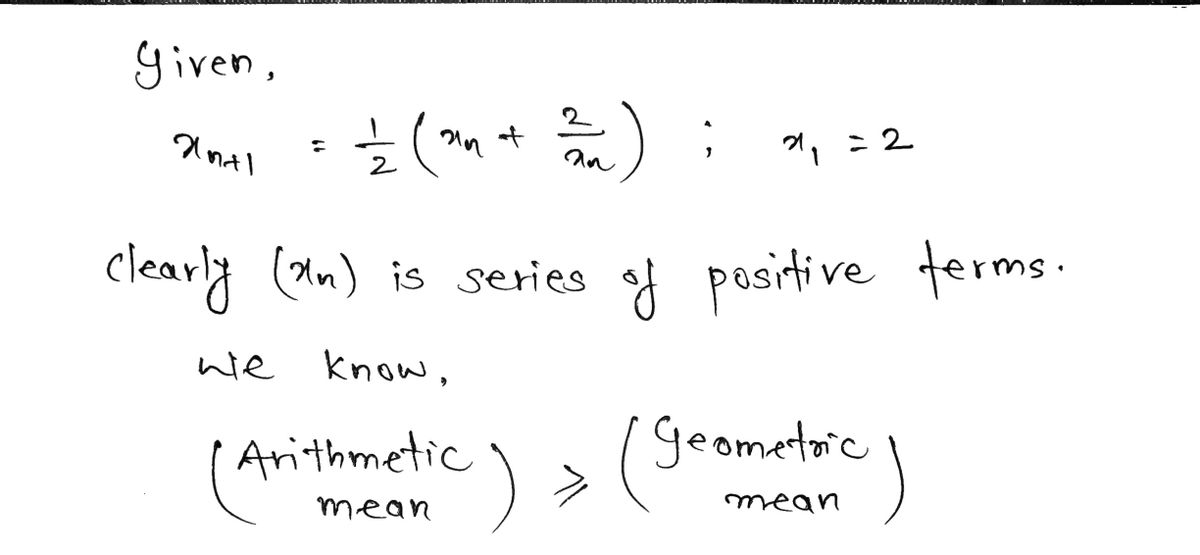
Step by step
Solved in 3 steps with 4 images
Recommended textbooks for you
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage