
Concept explainers
1. Introduction
Truss structures are essential in engineering applications due to their ability to efficiently distribute loads
and provide structural stability. Comprising triangular arrangements of linear members connected at
joints trusses efficiently carry axial loads, making them a popular choice for supporting roofs, bridges, and
towers. These structures are valued for their strength-to-weight ratio, which allows for the use of lighter
and more cost-effective materials without compromising overall stability.
2. Problem Statement
Figure 1 depicts a truss that forms part of the railroad bridge crossing the Connecticut River at Warehouse
Point in East Windsor, Connecticut. Constructed by the New York, New Haven & Hartford Railroad in the
early 1900s, this seven-panel structure incorporates Baltimore- and Pratt-style trusses elements. The floor
system is connected to the joints of the bottom horizontal members (or chords) and is supported by
hangers suspended from the mid-panel points. The middle three panels feature diagonal counters, lending
these panels a distinctive "X" shape.
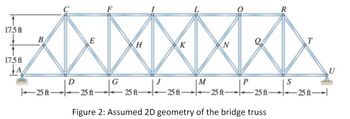
Consider the geometry depicted in Figure 2, representing one side of the truss. For the sake of clarity, the
mid-panel hangers have been omitted since they are zero-force members for both load cases. (Can you
identify any other zero-force members present?)
3. Assignments
Introduction. As a structural engineer, the objective is to determine the force developed in member CF
due to the train load to design the member. The live load on the bridge (i.e., train weight) is a moving
load, and as a result, the internal force of member CF can vary depending on the train's location. The
solution to a moving-load problem is to draw the influence line for member CF. The influence line of
member CF represents the variation of the internal force in this member as a unit point load moves from
joint A to U (this process models the concept of the train moving from point A to U).
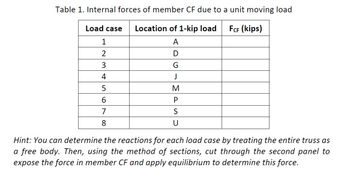
Task 1. Apply a unit load (1 kip) to each of the joints along the lower chord, starting at joint A and moving
to joints D, G, J, M, P, S, and U. The unit load at each location can be considered a load case. Thus, there
are 8 load cases, as presented in Table 1. Calculate the internal force of member CF for each load case and
complete this table. (Table in Photo Table.1)
Table 1. Internal forces of member CF due to a unit moving load
Hint: You can determine the reactions for each load case by treating the entire truss as
a free body. Then, using the method of sections, cut through the second panel to
expose the force in member CF and apply equilibrium to determine this force.
Task 2. Plot the results of the analysis from Task 1, with a vertical axis representing the internal force of
member CF and a horizontal axis representing the location of each joint relative to joint A.
This plot, referred to as an influence line, illustrates the force generated in member CF as a unit load
moves across the deck. Influence lines are crucial instruments for bridge design, allowing engineers to
examine the structural impacts of shifting loads. While they are created using a single unit force, methods
are available to apply these plots in assessing multiple-axle loads, such as the train depicted in Figure 1.
Task 3. Prepare a report that summarizes all your works in Tasks 1 and 2 including diagrams, detailed
calculations, and necessary discussions to support your analysis.
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 6 images

- (a) What is the effect of increasing the carbon content in steel on each of the each of the following items? 1. Yield strength 2. Modulus of elasticity 3. Ductility (b) Materials are generally classified into three categories based on the predominant types of bond. What are these three categories and what are the predominant types of bond in each category? For each category, provide two examples of common materials used by civil engineers.arrow_forwardProblem 6: The compound bar containing steel, bronze, and aluminum segments carries the axia! loads shown in the figure. The properties of the segments and the working stresses are listed in the table. Steel 2 ft Bronze 4 ft A (in.²) E (psi) o, (psi) Aluminum 3 ft 2P Steel 0.75 30 × 106 20 000 Bronze 1.00 12 x 106 18 000 4P Aluminum 0.50 10 x 106 12 000 Determine the maximum allowable value of P if the change in length of the entire bar is limited to 0.08 in. and the working stresses are not to be exceeded.arrow_forwardvalue for modulus of elasticty for steel is 29000 ksi and for aluminum it is 10000ksi. yield strength for steel is 36 ksi and yield strength for aluminum is 37 ksiarrow_forward
- Briefly identify what requirement of the strength is for a structural system and for a member of a structure.arrow_forwardGlu-laminated beams are used to support the roof and pulley load at a warehouse. Beams span 24 feet plus an eight foot overhang over the loading area. Determine the bending stress adequacy of the beam.arrow_forward

 Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON
Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
 Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning





