24. A particle moves along the x-axis so that at any time t20, its velocity is given by v(t)=cos(2-r'). The position of the particle is 3 at time t=0. What is the position of the particle when its velocity is first equal to 0? (A) 0.411 (B) 1.310 (C) 2.816 (D) 3.091 (E) 3.411
24. A particle moves along the x-axis so that at any time t20, its velocity is given by v(t)=cos(2-r'). The position of the particle is 3 at time t=0. What is the position of the particle when its velocity is first equal to 0? (A) 0.411 (B) 1.310 (C) 2.816 (D) 3.091 (E) 3.411
Related questions
Question
Please do all three part of these question. Thank you for your help.
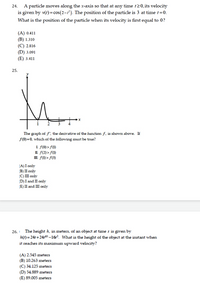
Transcribed Image Text:24. A particle moves along the x-axis so that at any time 120, its velocity
is given by v(r) = cos(2-r²). The position of the particle is 3 at time t=0.
What is the position of the particle when its velocity is first equal to 0?
(A) 0.411
(B) 1.310
(C) 2.816
(D) 3.091
(E) 3.411
25.
The graph of f. the derivative of the function f. is shown above. If
F(0)=0, which of the following must be true?
1 f(0) > f)
II f(2) > S)
m f(1)> f(3)
(A) I only
(B) II only
(C) I only
D) I and II only
(E) II and III only
26. The height h, in meters, of an object at time t is given by
h(1) = 24t +24: –16r?. What is the height of the object at the instant when
it reaches its maximum upward velocity?
(A) 2.545 meters
(B) 10.263 meters
(C) 34.125 meters
(D) 54.889 meters
(E) 89.005 meters
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps
