Question
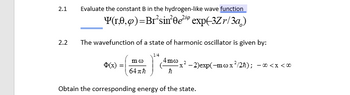
Transcribed Image Text:2.1
2.2
Evaluate the constant B in the hydrogen-like wave function
Y(1,0,0)=Br²sin²0e²¹⁹ exp(-3Zr/3a)
The wavefunction of a state of harmonic oscillator is given by:
1/4
$(x) =
mo
64πħ
4mo
ħ
x²-2)exp(-m cox ²/2ħ);
Obtain the corresponding energy of the state.
- 00 < x < 00
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps with 2 images

Knowledge Booster
Similar questions
- 1. Given the following probability density function: p(x) = Ae¬^(x-a)². 2. A particle of mass, m, has the wavefunction given by: Þ(x,t) = Ce-a[(mx²/h) + it] . 3. In a few sentences, explain why it is impossible to calculate (p) in the first problem, whereas in the second problem this is straightforward. Highlight the key concepts that differentiate these problems.arrow_forwardIn the following questions, we will use quantum states made up of the hydrogen energy eigenstates: Q1: Consider the election in a hydrogen atom to initially be in the state: F A. B. C. a) What is the probability of measuring the energy of this state and obtaining E₂? √3 √ vnim (r0,0)=R(r)Y," (0,0) always Y(t = 0) = √3 R₁OYO at t=0 but something different at t>0 ² at t=0 but something different at t>0 D. always 3 + E. Something else. b) Explain your answer. R₂₁ + R32Y₂¹arrow_forwardI am having trouble with solving this problem. Please show me how to solve it.arrow_forward