Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Related questions
Question
2.) Which graph is the daily case for New York?
a. I
b. II
c. III
d. IV
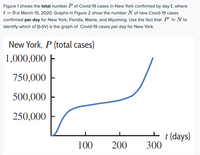
Transcribed Image Text:**Figure Description**
This figure is titled "New York, \( P \) (total cases)" and depicts a graph of the total number of COVID-19 cases confirmed in New York over time. The x-axis represents time \( t \) in days, starting from \( t = 0 \) on March 15, 2020. The y-axis represents the total number of COVID-19 cases, ranging from 0 to 1,000,000.
**Graph Analysis**
1. **X-Axis (Time in Days)**: The graph spans from 0 to approximately 350 days.
2. **Y-Axis (Total Cases)**: The scale ranges from 0 to 1,000,000 total cases.
3. **Graph Shape**: The curve starts near the origin, indicating few cases initially. It then rises steeply, particularly between day 50 to 100, and levels off slightly before rising sharply again after approximately day 250.
**Purpose**
The aim of this figure is to show the progression of total COVID-19 cases in New York over a period of time starting from March 15, 2020. The information will be used in conjunction with Figure 2 to determine which graph represents the daily new cases \( N \) for New York, using the relationship \( P' \approx N \).
**Educational Implications**
Understanding this graph helps illustrate how COVID-19 spread over time in New York, which is crucial for analyzing pandemic trends and healthcare responses. It provides a basis for comparison with other states' data in Figure 2.
**Note for Inclusion in Educational Website**
When presenting this information on an educational website, it is essential to include the context of the data, such as the time frame and specific location, to enhance comprehension and facilitate comparison with other datasets.
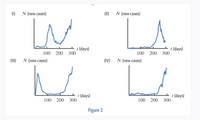
Transcribed Image Text:The image contains four graphs (labeled I, II, III, and IV) showing the number of new cases \( N \) over time \( t \) in days.
- **Graph I**: This graph shows fluctuating increases and decreases in new cases, with two significant peaks occurring around day 150 and day 300.
- **Graph II**: This graph illustrates a sharp increase in new cases with a single peak around day 250, followed by a rapid decline.
- **Graph III**: This graph depicts an initial steep peak in new cases at around day 50, followed by a decrease and then a gradual rise leading to another increase near day 300.
- **Graph IV**: This graph shows a prolonged period of low new cases, followed by a consistent increase beginning around day 250, trending steeply upward.
**Figure 2**: The graphs demonstrate different patterns of disease spread over approximately a one-year period, highlighting varying dynamics in outbreak progression.
Expert Solution
arrow_forward
Step 1
Please see the below picture for detailed solution.
Step by stepSolved in 2 steps with 1 images
Knowledge Booster
Similar questions
- Q6. Which of these statements are correct? I. In a bar graph the horizontal axis has categorical data and a histogram has numerical intervals. In a bar graph the frequency is depicted by the height of the bar. In a histogram the I. frequency is depicted by the area of the bar. II. In a bar chart the bars can have gaps between them but in a histogram the bars have no spaces between them. A. I. & II. B. II. & III. C. I. & III. D. I. & II. & I. O A. A В. В О С. С O D. Darrow_forward2. The table below shows the number of pounds of each snack food eaten during the during NBA Finals. Construct a pie graph for the data. Snack Pounds (frequency) Potato chips Tortilla chips 11.2 million 8.2 million Pretzels 4.3 million Popcorn Snack nuts 3.8 million 2.5 million Total n= 30.0 millionarrow_forwardHelparrow_forward
- Direction: Answer the following questions and graph. 1. Suppose there are 10, 000 test takers of the IQ test where the mean w=100 and Ihe slarndard devialion o=16. a) What are the raw scores that correspond to each of the following z scores? T. zl 2. 7=-1 3. 2=2 1. z 2 b) How many scores are Ihere above 84?arrow_forward5) Construct a Bar Graph illustrating the information provided in the chart. Label the vertical axis and horizontal axis accordingly Construct the bar graph Provide an appropriate title for the bar graph Desserts Number of People Cookies 8. 10 Ice Cream Cake 3 Pie Fudgearrow_forwardanswers only. Which of the following study is Inferential Statistics? a. 35% of the Enrolled Students in Maharlika University are Solo Parents. b. The market researcher of a manufacturing company constructs a graph showing the fluctuations in sales for a major product line during the past two years. c. The guard on duty recorded the students who came in with above 37.5 body temperature d. The manager of a department store records the number of buying customers daily for 7 consecutive weeks and then estimates the average number of buying customers for the following weeks. 2. What is the sample size of a certain study if the population size is 1,000,000 and 10% margin of error are expected? a.400 c,200 b.300 d.100 3.Which of the following examples is secondary data? a.Direct Interview c.journals b.Indirect or Questionnaire d.Observationarrow_forward
- 2.4 terlashow Worksheet 4.5 3. A car dealership is analyzing the changes in its monthly sales. They sold 40 cars in March, 55 in April, 61 in May, 29 in June, 63 in July, and 40 in August. Create line graph that represents this data. emait yerty bisz Sanco efimy svib AI 360 bar & svart 0.160 and to toloo er viunebi of bades new sinobuta SA 160 salsa.nolo3 1aritons esw 163 tiert bisz gniniemen sdt bns as old sved Ofic nong saved stab aid atangan ter dosarrow_forwardWhich of the following is correct about graphs? a. Requires drawing skill b. Depict categorical and geographic data c. Drawn on plain paper d. Furnish more accurate informationarrow_forward7. The following circle graph shows the distribution of expenditures related to wildlife watching in a recent year. Use the graph to answer the questions. Food Other 7% Lodging 5% 18% Transportation 7% Trip related costs 2% Equipment 61% a) What percent of expenditures are on food? b) In a recent year, $38 million was spent in wildlife watching recreation. How much of that was spent on transportation?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON 
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning