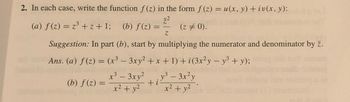
2. In each case, write the function f(z) in the form f(z) = u(x, y) + iv(x, y): z² (a) f(z)=z³+z+1; (b) f(z) = == (z =0). Suggestion: In part (b), start by multiplying the numerator and denominator by z. Ans. (a) f(z) = (x³ - 3xy² + x + 1) +i (3x²y - y³ + y); x3 - 3ху2 y³ - 3x²y x² + y² x² + y² (b) f(z) = +i Z

2. Consider the function f(x) = 4 – x². (a) Draw a sketch of the graph of the function. (b) Find the slope of the secant line connecting the points P(1, 3) and Q(2,0) on the graph. (c) Find the slope of the secant line connecting the points P(1,3) and Q(x,4 – x²). (d) Use algebra to simplify your formula from part (c) as much as possible, assuming that P and Q are distinct points. (e) What value do you get when you plug x = 1 into the simplified expression you found in part (d)? (f) Assume that your answer in part (e) is the slope of the tangent line to the graph y = 4 – x2 at the point P(1,3). Use that information to write an equation for the tangent line to the graph y = 4 – a² at the point P(1,3).

Evaluate f(x) = x°+6x, (fof)(3) =? O 91,395 O 2025 O 45 O 90

do only A). Find the composition of function and its domain.

2. Given the function f (x) = Vx, sketch the parent function and f(x) = -2/(x + 3)+4 by using mapping notation: %3D