
Trigonometry (11th Edition)
11th Edition
ISBN: 9780134217437
Author: Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
![**Title: Finding the Tangent of an Angle α**
**Objective:**
Learn how to find the tangent of an angle given a point on the coordinate plane.
**Concept Overview:**
In this diagram, we are tasked with finding the tangent of the angle α, which is formed by a vector \( r \) originating from the origin and terminating at the point \((\sqrt{5}, -\sqrt{7})\).
**Diagram Explanation:**
- A coordinate plane is depicted with both horizontal and vertical axes.
- The vector \( r \) makes an angle α with the horizontal axis.
- The coordinates of the endpoint of the vector are \((\sqrt{5}, -\sqrt{7})\).
**Steps to Find \(\tan \alpha\):**
The tangent of an angle in a right triangle is the ratio of the opposite side to the adjacent side:
\[
\tan \alpha = \frac{\text{Opposite}}{\text{Adjacent}}
\]
For a point \((x, y)\),
- \(\tan \alpha = \frac{y}{x}\)
Plugging in the coordinates:
- \(\tan \alpha = \frac{-\sqrt{7}}{\sqrt{5}}\)
**Conclusion:**
The tangent of angle α is \(\frac{-\sqrt{7}}{\sqrt{5}}\), which simplifies the trigonometric analysis of the vector in relation to the coordinate plane. Understanding this ratio is fundamental in relating algebraic expressions to geometric representations in trigonometry.](https://content.bartleby.com/qna-images/question/6f2c9438-5a89-4288-b691-8fe1dc913be9/45983d51-3efe-4b67-80e7-ee224c930312/holypvm_thumbnail.png)
Transcribed Image Text:**Title: Finding the Tangent of an Angle α**
**Objective:**
Learn how to find the tangent of an angle given a point on the coordinate plane.
**Concept Overview:**
In this diagram, we are tasked with finding the tangent of the angle α, which is formed by a vector \( r \) originating from the origin and terminating at the point \((\sqrt{5}, -\sqrt{7})\).
**Diagram Explanation:**
- A coordinate plane is depicted with both horizontal and vertical axes.
- The vector \( r \) makes an angle α with the horizontal axis.
- The coordinates of the endpoint of the vector are \((\sqrt{5}, -\sqrt{7})\).
**Steps to Find \(\tan \alpha\):**
The tangent of an angle in a right triangle is the ratio of the opposite side to the adjacent side:
\[
\tan \alpha = \frac{\text{Opposite}}{\text{Adjacent}}
\]
For a point \((x, y)\),
- \(\tan \alpha = \frac{y}{x}\)
Plugging in the coordinates:
- \(\tan \alpha = \frac{-\sqrt{7}}{\sqrt{5}}\)
**Conclusion:**
The tangent of angle α is \(\frac{-\sqrt{7}}{\sqrt{5}}\), which simplifies the trigonometric analysis of the vector in relation to the coordinate plane. Understanding this ratio is fundamental in relating algebraic expressions to geometric representations in trigonometry.
Expert Solution
arrow_forward
Step 1
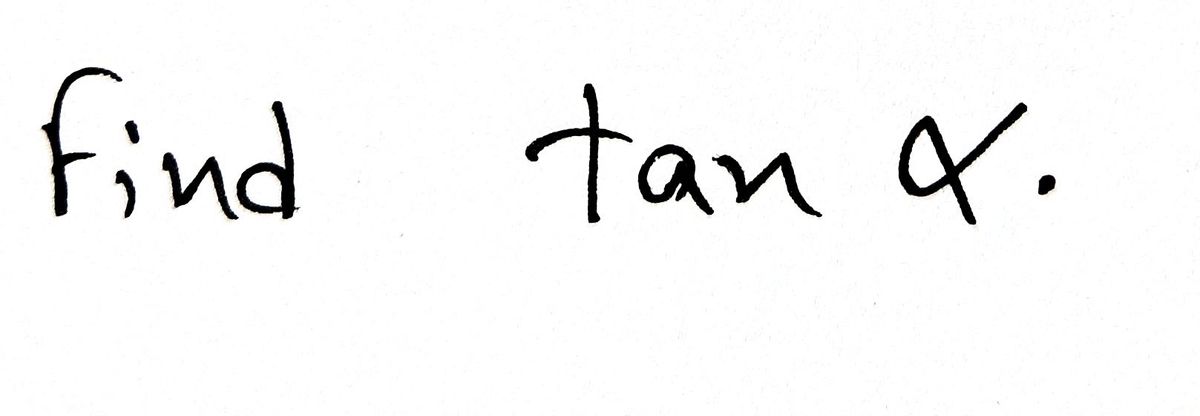
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Let X ~ N(-2, 5). Which of the following is equal to P(X > 0)? O ¤(2) 01-Ф(2/5) O ¤(2/v5). O ¤(-2/v5).arrow_forwardProblem YOUDEN RECTANGLE'S PROBLEM BIBD- Balanced Incomplete Block Design . There is a matrix m x n. This matrix can be 26 x 4 but we can change this dimension if 26 x 4 does not admit a feasible solution. • m> n + 1 • The rows are called "blocks" and the columns are called "forms" • Every form is composed by the same number of blocks • • Every block is composed by the same number of forms The matrix is full and every single spot should be filled with a treatment Every treatment is is replicated r times in the Youden rectangle • Every treatment appears in every form maximum one time • Every couple of treatment appear together in every form 1 times Every treatment appear in all single blocks the same number of times v = number of treatments (1,2,3,4,.....,n) n = blocks (columns) m = forms (rows) r = number of times every treatment is replicated λ = number of times two treatment appear together in the same form Constraints: 1) nxm=vxr - 2) 1 (v 1) = r (k-1) 3) m > v then r > n Goal The…arrow_forward-dæl V16-x*arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Trigonometry (11th Edition)TrigonometryISBN:9780134217437Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie DanielsPublisher:PEARSON
Trigonometry (11th Edition)TrigonometryISBN:9780134217437Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie DanielsPublisher:PEARSON Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning

Trigonometry (11th Edition)
Trigonometry
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning